如图，已知AB是⊙O的直径，点C、D在⊙O上，过D点作PF∥AC交⊙O于F，交AB于点E，∠BPF=∠ADC．
（1）求证：BP是⊙O的切线；
（2）求证：AE•EB=DE•EF；
（3）当⊙O的半径为
，AC=2，BE=1时，求BP的长．
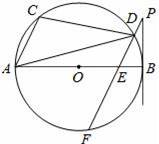
如图，已知AB是⊙O的直径，点C、D在⊙O上，过D点作PF∥AC交⊙O于F，交AB于点E，∠BPF=∠ADC．
（1）求证：BP是⊙O的切线；
（2）求证：AE•EB=DE•EF；
（3）当⊙O的半径为，AC=2，BE=1时，求BP的长．
【考点】切线的判定；相似三角形的判定与性质．
【分析】（1）根据圆周角定理得出∠ACB=90°，∠CAB+∠ABC=90°，进而得出∠PEB+∠BPF=90°，从而证得PB是ʘO的切线；
（2）证得△AEF∽△DEB，从而得出
=
，即可证得AE•EB=DE•EF；
（3）先根据勾股定理求得BC的长，进而根据△ABC∽△EPB，对应边成比例即可求得BP的长．
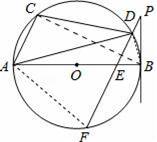
【解答】（1）证明：连结BC，
∵AB是ʘO的直径，
∴∠ACB=90°，
∴∠CAB+∠ABC=90°，
又∵∠ABC=∠ADC，∠ADC=∠BPF，
∵PF∥AC，
∴∠CAB=∠PEB，
∴∠PEB+∠BPF=90°，
∴PB⊥AB，
∴PB是ʘO的切线；
（2）连结AF、BD．
在△AEF和△DEB中，
∠AEF=∠DEB．∠AFE=∠DBE，
∴△AEF∽△DEB，
∴=，即AE•EB=DE•EF；
（3）在Rt△ABC中，BC2=（2
）2﹣22
∴BC=4，
在Rt△ABC和Rt△EPB中，
∠ABC=∠ADC=∠BPF，
∴△ABC∽△EPB，
∴
=
，
∴BP=
=2．
【点评】本题考查了切线的判定，三角形相似的判定和性质，勾股定理的应用等，熟练掌握性质定理是解题的关键．