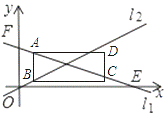
如图，在平面直角坐标系中，点F的坐标为（0，10）．点E的坐标为（2

如图，在平面直角坐标系中，点F的坐标为（0，10）．点E的坐标为（20，0），直线l₁经过点F和点E，直线l₁与直线l₂ 、y=x相交于点P．

（1）求直线l₁的表达式和点P的坐标；

（2）矩形ABCD的边AB在y轴的正半轴上，点A与点F重合，点B在线段OF上，边AD平行于x 轴，且AB=6，AD=9，将矩形ABCD沿射线FE的方向平移，边AD始终与x 轴平行．已知矩形ABCD以每秒个单位的速度匀速移动（点A移动到点E时止移动），设移动时间为t秒（t＞0）．

①矩形ABCD在移动过程中，B、C、D三点中有且只有一个顶点落在直线l₁或l₂上，请直接写出此时t的值；

②若矩形ABCD在移动的过程中，直线CD交直线l₁于点N，交直线l₂于点M．当△PMN的面积等于18时，请直接写出此时t的值．

【解答】解：（1）设直线l₁的表达式为y=kx+b

∵直线l₁过点F（0，10），E（20，0）

∴

解得

直线l₁的表达式为y=﹣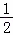x+10

求直线l₁与直线l₂ 交点，得

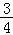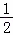x=﹣x+10

解得x=8

y=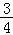×8=6

∴点P坐标为（8，6）

（2）①如图，当点D在直线上l₂时

∵AD=9

∴点D与点A的横坐标之差为9

∴将直线l₁与直线l₂ 交解析式变为

x=20﹣2y，x=y

∴y﹣（20﹣2y）=9

解得

y=

则点A的坐标为：（，）

则AF=

∵点A速度为每秒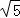个单位

∴t=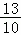

如图，当点B在l₂ 直线上时

∵AB=6

∴点A的纵坐标比点B的纵坐标高6个单位

∴直线l₁的解析式减去直线l₂ 的解析式得

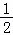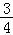﹣x+10﹣x=6

解得x=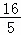

则点A坐标为（，）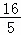

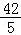则AF=

∵点A速度为每秒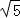个单位

∴t=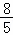

故t值为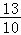或

②如图，

设直线AB交l₂ 于点H

设点A横坐标为a，则点D横坐标为a+9

由①中方法可知：MN=

此时点P到MN距离为：

a+9﹣8=a+1

∵△PMN的面积等于18

∴

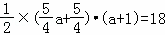
解得

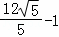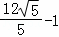a₁=，a₂=﹣（舍去）

∴AF=6﹣

则此时t为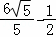

当t=时，△PMN的面积等于18

【点评】本题是代数几何综合题，应用待定系数法和根据函数关系式来表示点坐标，涉及到了分类讨论思想和数形结合思想．