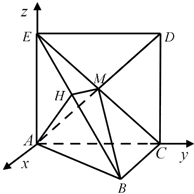
如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC

如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC．

（Ⅰ）求证：AM⊥平面EBC；

（Ⅱ）求二面角A﹣EB﹣C的大小．

【考点】用空间向量求平面间的夹角；直线与平面垂直的判定．

【专题】空间位置关系与距离；空间角．

【分析】几何法：

（Ⅰ）由已知得AM⊥EC，AC⊥BC，由此能证明AM⊥平面EBC．

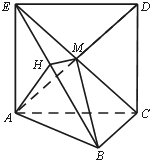
（Ⅱ）过A作AH⊥EB于H，连结HM，由已知得∠AHM是二面角A﹣EB﹣C的平面角，由此能求出二面角A﹣EB﹣C的大小．

向量法：

（Ⅰ）以点A为原点，以过A点平行于BC的直线为x轴，分别以直线AC和AE为y轴和z轴，建立空间直角坐标系A﹣xyz，利用向量法能证明AM⊥平面EBC．

（2）求出平面EAB的法向量和平面EBC的法向量，利用向量法能求出二面角A﹣EB﹣C的大小．

【解答】（本小题满分12分）

几何法：

（Ⅰ）证明：∵四边形ACDE是正方形，∴AM⊥EC，

又∵平面ACDE⊥平面ABC，∴AC⊥BC，

∴BC⊥平面EAC，…

∵BC⊄平面EAC，∴BC⊥AM，

又∵EC∩BC=C，∴AM⊥平面EBC．…

（Ⅱ）解：过A作AH⊥EB于H，连结HM，

∵AM⊥平面EBC，∴AM⊥EB，∴EB⊥平面AHM，

∴∠AHM是二面角A﹣EB﹣C的平面角，…

∵平面ACDE⊥平面ABC，∴EA⊥平面ABC，∴EA⊥AB，

在Rt△EAB中，AH⊥EB，有AE•AB=EB•AH，

设EA=AC=BC=2a，得，AB=2a，EB=2a，∴=，

∴sin=，∴∠AHM=60°．

∴二面角A﹣EB﹣C等于60°．…

向量法：

（Ⅰ）证明：∵四边形ACDE是正方形，∴EA⊥AC，

∵平面ACDE⊥平面ABC，EA⊥平面ABC，…

∴以点A为原点，以过A点平行于BC的直线为x轴，

分别以直线AC和AE为y轴和z轴，

建立如图所示的空间直角坐标系A﹣xyz，

设EA=AC=BC=2，则A（0，0，0），C（0，2，0），E（0，0，2），

M是正方形ACDE的对角线的交点，M（0，1，1），…

=（0，1，1），=（0，2，﹣2），，

∴，∴AM⊥EC，AM⊥BC，

又EC∩BC=C，∴AM⊥平面EBC．…

（2）设平面EAB的法向量为，则，

∴，取y=﹣1，则x=1，则=（1，﹣1，0），…

又∵为平面EBC的一个法向量，

∴cos＜＞==﹣，

设二面角A﹣EB﹣C的平面角为θ，则cosθ=|cos＜＞|=，∴θ=60°，

∴二面角A﹣EB﹣C等于60°．…

【点评】本题考查直线与平面垂直的证明，考查二面角的大小的求法，解题时要认真审题，注意空间思维能力的培养．