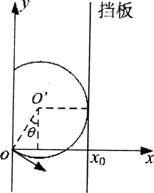
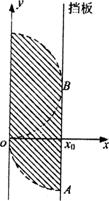
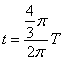如题l3-l图所示的坐标系内，在x0(x0>0)处有一垂直工轴放置的挡板．在y轴与挡板之间的区域内存在一个与xoy平珏垂直且指向纸内的匀强磁场，磁感应强度B=0．2T．位于坐标原点O处的粒子源向xoy平面内发射出大量同种带正电的粒子，所有粒子的初速度大小均为vo=1.0×106m/s，方向与x轴正方向的夹角为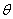
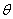，且0≤≤90°．该粒子的比荷为
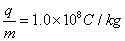，不计粒子所受重力和粒子间的相互作用，粒子打到挡板上后均被挡板吸收．
(1)求粒子在磁场中运动的轨道半径R：
(2)如题l3-2图所示，为使沿初速度方向与x轴正方向的夹角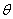=30°射出的粒子不打到挡板上，则x0必须满足什么条件?该粒子在磁场中运动的时间是多少?
(3)若x0=5.0×10-2m，求粒子打在挡板上的范围(用y坐标表示)，并用“
”图样在题l3-3图中画出粒子在磁场中所能到达的区域：
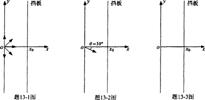
解：(1)由牛顿第二定律得
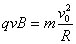……………………………………………………………………………(2分)
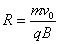=5.0×10-2m………………………………………………………………(1分)
(2)如图所示，设粒子的运动轨迹恰与挡板相切，由几何关系得：
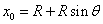……………………………………………………………………………(2分)
X0=7.5×10-2m…………………………………………………………………………(1分)
为使该粒子不打到挡板上，x0≥7.5×10-2m………………………………………(1分)
粒子在磁场中运动的周期为T
T=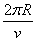
=
=
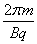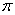×10-7s…………………………………………………………(1分)
该粒子在磁场中运动的时间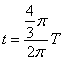
=
=
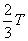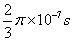……………………(1分)
(3)若x0=5.0×10-2m，则x0=R
当粒子沿着－y方向入射时，将打在挡板上的A点
其纵坐标yA=－R=500×10-2m…………………………………………………(2分)
当粒子沿着+x方向入射时，粒子的运动轨迹恰好与挡板相切于B点
其纵坐标yB=R=5.0×10-2m……………………………………………………(2分)
则粒子打在挡板上的范围为-500×10-2m≤y<5.0×10-2m…………………(1分)
粒子在磁场中所能到达的区域如图所示………………………………………(4分)
