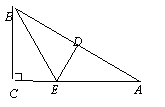
如图，已知Rt△ABC中，∠C=90°．沿DE折叠，使点A与点B重合，
折痕为DE．
（1）若DE=CE，求∠A的度数 ；
（2）若BC=6，AC=8，求CE的长．
如图，已知Rt△ABC中，∠C=90°．沿DE折叠，使点A与点B重合，
折痕为DE．
（1）若DE=CE，求∠A的度数 ；
（2）若BC=6，AC=8，求CE的长．
（1）解：∵折叠使点A与点B重合，折痕为DE．
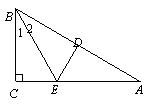∴DE垂直平分AB．
∴AE=BE， …………… 1分
∴∠A＝∠2
又∵DE⊥ AB，∠C=90°，DE=CE，
∴∠1＝∠2，
∴∠1＝∠2=∠A．
由∠A+∠1+∠2=90°，解得：∠A=30°
（2）解：设CE =x，则AE=BE=8-x．
在Rt△BCE中，由勾股定理得：BC2+ CE 2= BE2．
即 62+x2 = (8-x)2，
解得：x=
， 即CD=．