已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,其右焦点为
,其右焦点为![]() ,过点
,过点![]() 作直线交椭圆于另一点
作直线交椭圆于另一点![]() .
.
(1)若![]() ,求
,求![]() 外接圆的方程;
外接圆的方程;
(2)若过点![]() 的直线与椭圆
的直线与椭圆![]()
![]() 相交于两点
相交于两点![]() 、
、![]() ,设
,设![]() 为
为![]() 上一点,且满足
上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,其右焦点为
,其右焦点为![]() ,过点
,过点![]() 作直线交椭圆于另一点
作直线交椭圆于另一点![]() .
.
(1)若![]() ,求
,求![]() 外接圆的方程;
外接圆的方程;
(2)若过点![]() 的直线与椭圆
的直线与椭圆![]()
![]() 相交于两点
相交于两点![]() 、
、![]() ,设
,设![]() 为
为![]() 上一点,且满足
上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
解:(1)由题意知:![]() ,
,![]() ,又
,又![]() ,
,
解得:![]()
![]() 椭圆
椭圆![]() 的方程为:
的方程为:![]() 2分
2分
可得:![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,即
,即![]()
由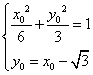
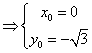 ,或
,或
即![]() ,或
,或![]() 4分
4分
①当![]() 的坐标为
的坐标为![]() 时,
时,![]() ,
,![]()
![]() 外接圆是以
外接圆是以![]() 为圆心,
为圆心,![]() 为半径的圆,即
为半径的圆,即![]() 5分
5分
②当![]() 的坐标为
的坐标为![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 为直角三角形,其外接圆是以线段
为直角三角形,其外接圆是以线段![]() 为直径的圆,圆心坐标为
为直径的圆,圆心坐标为![]() ,半径为
,半径为![]() ,
,
![]() 外接圆的方程为
外接圆的方程为![]()
综上可知:![]() 外接圆方程是
外接圆方程是![]() ,或
,或![]() 6分
6分
(2)由题意可知直线![]() 的斜率存在.
的斜率存在.
设![]() ,
,![]() ,
,![]() ,
,![]()
由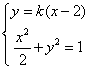 得:
得:![]()
由![]() 得:
得:![]() (
(![]() ) 8分
) 8分
![]()
![]() ,
,![]() 即
即![]()
![]() ,结合(
,结合(![]() )得: 10分
)得: 10分
![]() ,
,![]()
从而![]() ,
,![]()
![]() 点
点![]() 在椭圆上,
在椭圆上,![]() ,整理得:
,整理得:![]()
即![]() ,
,![]() ,或
,或![]() 12分
12分