已知函数
．
（1）若曲线
与曲线
在它们的交点
处具有公共切线，求
的值；
（2）当
时，若函数
在区间
上的最大值为28，求
的取值范围．
已知函数．
（1）若曲线与曲线在它们的交点处具有公共切线，求的值；
（2）当时，若函数在区间上的最大值为28，求的取值范围．
(1)∵曲线y＝f(x)＝ax2＋1与曲线y＝g(x)＝x3＋bx交于点(1，c)
∴a+1=c，b+1=c
∴a=b………………………………………………………………………1分
∵f(x)＝ax2＋1(a＞0)
∴f′(x)＝2ax，f(1)＝a＋1
∴f′(1)＝2a
∴公切线方程为y－(a+1)＝2a(x－1)，即y=2ax－(a－1)…………3分
又∵g(x)＝x3＋bx
∴g′(x)＝3x2＋b，g(1)=b+1
∴g′(1)＝b+3
∴公切线方程为y－(b+1)＝(b+3)(x－1)，即y=(b+3)x－2………5分
比较两条公切线的方程知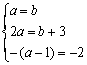
∴a＝b＝3.……………………………………………………………7分
(2)记h(x)＝f(x)＋g(x)，则当a＝3，b＝－9时，h(x)＝x3＋3x2－9x＋1
∴h′(x)＝3x2＋6x－9＝3(x+3)(x－1)……………………………8分
| x | (－∞，－3) | －3 | (－3，1) | 1 | (1，2) | 2 |
| h′(x) | ＋ | 0 | － | 0 | ＋ | |
| H(x) | ↗ | 28 | ↘ | －4 | ↗ | 3 |
…………………………………………………………………………10分
又∵函数h(x)在区间[k，2]上的最大值为28＝h(－3)
∴k的取值范围是(－∞，－3]．……………………………………12分