еҰӮеӣҫпјҢжӨӯеңҶ пјқ1(aпјһbпјһ0)зҡ„дёҠпјҢдёӢдёӨдёӘйЎ¶зӮ№дёәAпјҢBпјҢзӣҙзәҝlпјҡyпјқпјҚ2пјҢзӮ№PжҳҜжӨӯеңҶдёҠејӮдәҺзӮ№AпјҢBзҡ„д»»ж„ҸдёҖзӮ№пјҢиҝһжҺҘAP并延й•ҝдәӨзӣҙ
пјқ1(aпјһbпјһ0)зҡ„дёҠпјҢдёӢдёӨдёӘйЎ¶зӮ№дёәAпјҢBпјҢзӣҙзәҝlпјҡyпјқпјҚ2пјҢзӮ№PжҳҜжӨӯеңҶдёҠејӮдәҺзӮ№AпјҢBзҡ„д»»ж„ҸдёҖзӮ№пјҢиҝһжҺҘAP并延й•ҝдәӨзӣҙ зәҝlдәҺзӮ№NпјҢиҝһжҺҘPB并延й•ҝдәӨзӣҙзәҝlдәҺзӮ№MпјҢи®ҫAPжүҖеңЁзҡ„зӣҙзәҝзҡ„ж–ңзҺҮдёәk1пјҢBPжүҖеңЁзҡ„зӣҙзәҝзҡ„ж–ңзҺҮдёәk2.иӢҘжӨӯеңҶзҡ„зҰ»еҝғзҺҮдёә
зәҝlдәҺзӮ№NпјҢиҝһжҺҘPB并延й•ҝдәӨзӣҙзәҝlдәҺзӮ№MпјҢи®ҫAPжүҖеңЁзҡ„зӣҙзәҝзҡ„ж–ңзҺҮдёәk1пјҢBPжүҖеңЁзҡ„зӣҙзәҝзҡ„ж–ңзҺҮдёәk2.иӢҘжӨӯеңҶзҡ„зҰ»еҝғзҺҮдёә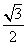 пјҢдё”иҝҮзӮ№A(0,1)пјҺ
пјҢдё”иҝҮзӮ№A(0,1)пјҺ

(1)жұӮk1В·k2зҡ„еҖјпјӣ
(2)жұӮMNзҡ„жңҖе°ҸеҖјпјӣ
(3)йҡҸзқҖзӮ№Pзҡ„еҸҳеҢ–пјҢд»ҘMNдёәзӣҙеҫ„зҡ„еңҶжҳҜеҗҰжҒ’иҝҮе®ҡзӮ№пјҹиӢҘиҝҮе®ҡзӮ№пјҢжұӮеҮәиҜҘе®ҡзӮ№пјӣеҰӮдёҚиҝҮе®ҡзӮ№пјҢиҜ·иҜҙжҳҺзҗҶз”ұпјҺ
и§ЈгҖҖ(1)еӣ дёәeпјқ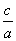 пјқ
пјқ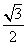 пјҢbпјқ1пјҢи§Јеҫ—aпјқ2пјҢжүҖд»ҘжӨӯеңҶCзҡ„ж ҮеҮҶж–№зЁӢдёә
пјҢbпјқ1пјҢи§Јеҫ—aпјқ2пјҢжүҖд»ҘжӨӯеңҶCзҡ„ж ҮеҮҶж–№зЁӢдёә пјқ1.(2еҲҶ)
пјқ1.(2еҲҶ)

и®ҫжӨӯеңҶдёҠзӮ№P(x0пјҢy0)пјҢжңү пјқ1пјҢ
пјқ1пјҢ
жүҖд»Ҙk1В·k2пјқ (2)еӣ дёәMпјҢNеңЁзӣҙзәҝlпјҡyпјқпјҚ2дёҠпјҢи®ҫM(x1пјҢпјҚ2)пјҢN(x2пјҢпјҚ2)пјҢ
(2)еӣ дёәMпјҢNеңЁзӣҙзәҝlпјҡyпјқпјҚ2дёҠпјҢи®ҫM(x1пјҢпјҚ2)пјҢN(x2пјҢпјҚ2)пјҢ
з”ұж–№зЁӢзҹҘ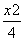 пјӢy2пјқ1зҹҘпјҢA(0,1)пјҢB(0пјҢпјҚ1)пјҢ
пјӢy2пјқ1зҹҘпјҢA(0,1)пјҢB(0пјҢпјҚ1)пјҢ
жүҖд»ҘKBMВ·kANпјқ (6еҲҶ)
(6еҲҶ)
еҸҲз”ұ(1)зҹҘkANВ·kBMпјқk1В·k2пјқпјҚ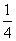 пјҢжүҖд»Ҙx1x2пјқпјҚ12пјҢ(8еҲҶ)
пјҢжүҖд»Ҙx1x2пјқпјҚ12пјҢ(8еҲҶ)
дёҚеҰЁи®ҫx1пјң0пјҢеҲҷx2пјһ0пјҢеҲҷ
MNпјқ|x1пјҚx2|пјқx2пјҚx1пјқx2пјӢ пјқ4
пјқ4 пјҢ
пјҢ
жүҖд»ҘеҪ“дё”д»…еҪ“x2пјқпјҚx1пјқ2 ж—¶пјҢMNеҸ–еҫ—жңҖе°ҸеҖј4
ж—¶пјҢMNеҸ–еҫ—жңҖе°ҸеҖј4 .(10еҲҶ)
.(10еҲҶ)
(3)и®ҫM(x1пјҢпјҚ2)пјҢN(x2пјҢпјҚ2)пјҢ
еҲҷд»ҘMNдёәзӣҙеҫ„зҡ„еңҶзҡ„ж–№зЁӢдёә
(xпјҚx1)(xпјҚx2)пјӢ(yпјӢ2)2пјқ0пјҢ(12еҲҶ)
еҚіx2пјӢ(yпјӢ2)2пјҚ12пјҚ(x1пјӢx2)xпјқ0пјҢиӢҘеңҶиҝҮе®ҡзӮ№пјҢ
еҲҷжңүxпјқ0пјҢx2пјӢ(yпјӢ2)2пјҚ12пјқ0пјҢи§Јеҫ—xпјқ0пјҢyпјқпјҚ2Вұ2 пјҢ
пјҢ
жүҖд»ҘпјҢж— и®әзӮ№PеҰӮдҪ•еҸҳеҢ–пјҢд»ҘMNдёәзӣҙеҫ„зҡ„еңҶжҒ’иҝҮе®ҡзӮ№(0пјҢпјҚ2Вұ2 )пјҺ(16еҲҶ)
)пјҺ(16еҲҶ)
![]() пјқ1(aпјһbпјһ0)зҡ„дёҠпјҢдёӢдёӨдёӘйЎ¶зӮ№дёәAпјҢBпјҢзӣҙзәҝlпјҡyпјқпјҚ2пјҢзӮ№PжҳҜжӨӯеңҶдёҠејӮдәҺзӮ№AпјҢBзҡ„д»»ж„ҸдёҖзӮ№пјҢиҝһжҺҘAP并延й•ҝдәӨзӣҙ
пјқ1(aпјһbпјһ0)зҡ„дёҠпјҢдёӢдёӨдёӘйЎ¶зӮ№дёәAпјҢBпјҢзӣҙзәҝlпјҡyпјқпјҚ2пјҢзӮ№PжҳҜжӨӯеңҶдёҠејӮдәҺзӮ№AпјҢBзҡ„д»»ж„ҸдёҖзӮ№пјҢиҝһжҺҘAP并延й•ҝдәӨзӣҙ![]() зәҝlдәҺзӮ№NпјҢиҝһжҺҘPB并延й•ҝдәӨзӣҙзәҝlдәҺзӮ№MпјҢи®ҫAPжүҖеңЁзҡ„зӣҙзәҝзҡ„ж–ңзҺҮдёәk1пјҢBPжүҖеңЁзҡ„зӣҙзәҝзҡ„ж–ңзҺҮдёәk2.иӢҘжӨӯеңҶзҡ„зҰ»еҝғзҺҮдёә
зәҝlдәҺзӮ№NпјҢиҝһжҺҘPB并延й•ҝдәӨзӣҙзәҝlдәҺзӮ№MпјҢи®ҫAPжүҖеңЁзҡ„зӣҙзәҝзҡ„ж–ңзҺҮдёәk1пјҢBPжүҖеңЁзҡ„зӣҙзәҝзҡ„ж–ңзҺҮдёәk2.иӢҘжӨӯеңҶзҡ„зҰ»еҝғзҺҮдёә![]() пјҢдё”иҝҮзӮ№A(0,1)пјҺ
пјҢдё”иҝҮзӮ№A(0,1)пјҺ

