新冠疫情期间，口罩成为了人们出行必备的防护工具．某药店三月份

新冠疫情期间，口罩成为了人们出行必备的防护工具．某药店三月份共销售A，B两种型号的口罩9000只，共获利润5000元，其中A，B两种型号口罩所获利润之比为2：3．已知每只B型口罩的销售利润是A型口罩的1.2倍．

（1）求每只A型口罩和B型口罩的销售利润；

（2）该药店四月份计划一次性购进两种型号的口罩共10000只，其中B型口罩的进货量不超过A型口罩的1.5倍，设购进A型口罩m只，这1000只口罩的销售总利润为W元．该药店如何进货，才能使销售总利润最大？

（1）每只A型口罩和B型口罩的销售利润分别为0.5元，0.6元；（2）药店购进A型口罩4000只、B型口罩6000只，才能使销售总利润最大，最大利润为5600元

【解析】

（1）设销售A型口罩x只，销售B型口罩y只，根据“药店三月份共销售A，B两种型号的口罩9000只，共获利润5000元，其中A，B两种型号口罩所获利润之比为2：3”列方程组解答即可；

（2）根据题意即可得出W关于m的函数关系式；根据题意列不等式得出m的取值范围，再结合根据一次函数的性质解答即可．

【详解】

解：设销售A型口罩x只，销售B型口罩y只，根据题意得：

，

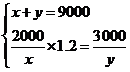解得，

经检验，x＝4000，y＝5000是原方程组的解，

∴每只A型口罩的销售利润为：（元），

每只B型口罩的销售利润为：0.5×1.2＝0.6（元），

答：每只A型口罩和B型口罩的销售利润分别为0.5元，0.6元．

（2）根据题意得，W＝0.5m+0.6（10000﹣m）＝﹣0.1m+6000，

10000﹣m≤1.5m，解得m≥4000，

∵0.1＜0，

∴W随m的增大而减小，

∵m为正整数，

∴当m＝4000时，W取最大值，则﹣0.1×4000+6000＝5600，

即药店购进A型口罩4000只、B型口罩6000只，才能使销售总利润最大，最大利润为5600元．

【点睛】

本题主要考查了一次函数的应用，二元一次方程组及一元一次不等式的应用，解题的关键是根据一次函数x值的增大而确定y值的增减情况．