和3,则点P到棱AB的距离为( ) A.
C. 
D.
和3,则点P到棱AB的距离为( ) A.
C. D.
解析:如图，过点P作PE⊥α于点E，PF⊥β于点F，则PE=
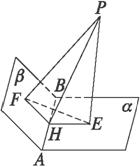
∵α∩β=AB,PE⊥α,PF⊥β,
∴AB⊥PE,AB⊥PF.
又PE∩PF=P，∴AB⊥平面PEF.
设AB∩平面PEF=H，连结EH、FH、PH、EF，则∠EHF为二面角αABβ的平面角，PH⊥AB,
即∠EHF=135°，PH长就是所求.
∵PE⊥α,PF⊥β,∴PE⊥EH,PF⊥FH.
从而P、E、H、F四点共圆.
∴∠FPE=180°-∠FHE=180°-135°=45°,并且PH为这个圆的直径.
在△PEF中，由余弦定理，得
EF=
在△EPF中，由正弦定理，得
PH=
因此点P到棱AB的距离为
答案:D