用火柴棒摆“金鱼”,如图所示:按照上面的规律,第n个“金鱼”图需要火柴棒的根数为( )
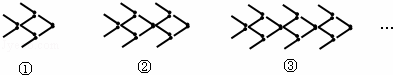
|
| A. | 6n﹣2 | B. | 8n﹣2 | C. | 6n+2 | D. | 8n+2 |
用火柴棒摆“金鱼”,如图所示:按照上面的规律,第n个“金鱼”图需要火柴棒的根数为( )
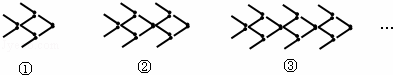
|
| A. | 6n﹣2 | B. | 8n﹣2 | C. | 6n+2 | D. | 8n+2 |
考点:
归纳推理.
专题:
规律型.
分析:
由图形间的关系可以看出,每多出一个小金鱼,则要多出6根火柴棒,则组成不同个数的图形的火柴棒的个数组成一个首项是8,公差是6的等差数列,写出通项,求出第n项的火柴根数.
解答:
解:∵第一个图中有8根火柴棒组成,
第二个图中有8+6个火柴棒组成,
第三个图中有8+2×6个火柴组成,
以此类推
组成n个系列正方形形的火柴棒的根数是8+6(n﹣1)
∴第n个图中的火柴棒有6n+2
故选C.
点评:
本题考查归纳推理,考查等差数列的通项,解题的关键是看清随着小金鱼的增加,火柴的根数的变化趋势,看出规律.