(本小题满分14分)
设数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,令
为公比的等比数列,令![]() ,
,![]() ,
,![]()
试用![]() 表示
表示![]() 和
和![]()
若![]() 且
且![]() ,试比较
,试比较![]() 与
与![]()
![]() 的大小
的大小
是否存在实数对![]() ,其中
,其中![]() ,使得
,使得![]() 成等比数列,若存在,求出实数对
成等比数列,若存在,求出实数对![]() 和
和![]() ;若不存在说明理由
;若不存在说明理由
(本小题满分14分)
设数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,令
为公比的等比数列,令![]() ,
,![]() ,
,![]()
试用![]() 表示
表示![]() 和
和![]()
若![]() 且
且![]() ,试比较
,试比较![]() 与
与![]()
![]() 的大小
的大小
是否存在实数对![]() ,其中
,其中![]() ,使得
,使得![]() 成等比数列,若存在,求出实数对
成等比数列,若存在,求出实数对![]() 和
和![]() ;若不存在说明理由
;若不存在说明理由
解:解:(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() ;………………2分
;………………2分
当![]() 时,
时,![]() ,
,![]() ----------------------------4分
----------------------------4分
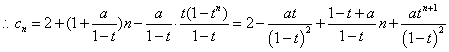 ----------------------------6分
----------------------------6分
(2)![]() ------------------7分
------------------7分
当![]() 时,
时,![]() ,而已知
,而已知![]() ,
,![]()
![]()
同理当![]() 时,
时,![]() ,而已知
,而已知![]() ,
,![]()
![]() ---------9分
---------9分
综上所述![]() ------10分
------10分
(3)若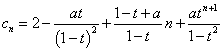 成等比数列,则令
成等比数列,则令 -------11分
-------11分
由(2),得![]() 代入(1),得
代入(1),得![]() ------------------13分
------------------13分
此时![]()
所以存在实数对![]() 为
为![]() ,使得
,使得![]() 成为以4为首项,2为公比的等比数列-------------14分
成为以4为首项,2为公比的等比数列-------------14分