．如图，AB是⊙O的切线，B为切点，AO的延长线交⊙O于C点，连接BC，如果∠A=30°，AB=2
，那么AC的长等于 ．
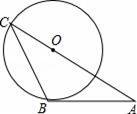
．如图，AB是⊙O的切线，B为切点，AO的延长线交⊙O于C点，连接BC，如果∠A=30°，AB=2，那么AC的长等于 ．
6 ．
【考点】切线的性质；解直角三角形．
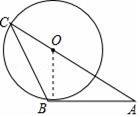
【分析】连接OB，则△AOB是直角三角形，利用三角函数即可求得OA的长，则AC即可求解．
【解答】解：连接OB．
∵AB是⊙O的切线，B为切点，
∴OB⊥AB，
在直角△OAB中，OB=AB•tanA=2
×
=2，
则OA=2OB=4，
∴AC=4+2=6．
故答案是：6．
【点评】本题考查了三角函数以及切线的性质，正确判断△OAB是直角三角形是关键．