如图，已知在△ABC中，cosA=
，BE、CF分别是AC、AB边上的高，联结EF，那么△AEF和△ABC的周长比为（ ）
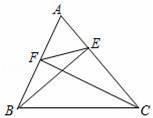
A．1：2 B．1：3 C．1：4 D．1：9
如图，已知在△ABC中，cosA=，BE、CF分别是AC、AB边上的高，联结EF，那么△AEF和△ABC的周长比为（ ）
A．1：2 B．1：3 C．1：4 D．1：9
B【考点】相似三角形的判定与性质．
【分析】由△AEF∽△ABC，可知△AEF与△ABC的周长比=AE：AB，根据cosA=
=
，即可解决问题．
【解答】解：∵BE、CF分别是AC、AB边上的高，
∴∠AEB=∠AFC=90°，
∵∠A=∠A，
∴△AEB∽△AFC，
∴
=
，
∴=
，∵∠A=∠A，
∴△AEF∽△ABC，
∴△AEF与△ABC的周长比=AE：AB，
∵cosA=
=
，
∴∴△AEF与△ABC的周长比=AE：AB=1：3，
故选B．
【点评】本题考查相似三角形的判定和性质，解题的关键是灵活运用相似三角形的性质解决问题，属于中考常考题型．