选修4－4：坐标系与参数方程
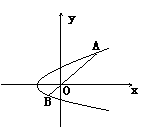已知抛物线
，过原点
作一直线交抛物线于
、
两点，如图所示，试求
的最小值.
选修4－4：坐标系与参数方程
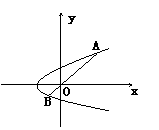
已知抛物线，过原点作一直线交抛物线于、两点，如图所示，试求的最小值.
解：法一：以原点为极点，x轴的正半轴为极轴，单位长度相同建立极坐标系，得抛物线y2=4a(x+a)的极坐标方程为
sin2
-4a
sin-4a2=0……4分
∴|OA||OB|=
……8分
当
时，|OA||OB|取最小值.……10分
法二：设直线AB的参数方程为
(t为参数). ……2分
代入y2=4a(x+a)中得：
sin2
-4atcos-4a2=0 ……6分
∴|OA||OB|=|t1t2|=
……8分
当
时，|OA||OB|取最小值.……10分