еҰӮеӣҫжүҖзӨәпјҢв–іABCдёәзӣҙи§’дёүи§’еҪўпјҢвҲ C=90В°пјҢиӢҘ![]() =(0пјҢ-4)пјҢMеңЁ
=(0пјҢ-4)пјҢMеңЁ![]() иҪҙдёҠпјҢдё”AM=
иҪҙдёҠпјҢдё”AM=![]() пјҢзӮ№CеңЁ
пјҢзӮ№CеңЁ![]() иҪҙдёҠ移еҠЁпјҺ
иҪҙдёҠ移еҠЁпјҺ
 В
В
(в… )жұӮзӮ№Bзҡ„иҪЁиҝ№Eзҡ„ж–№зЁӢ;В В
(в…Ў)иҝҮзӮ№F(0пјҢ![]() )зҡ„зӣҙзәҝ
)зҡ„зӣҙзәҝ![]() дёҺжӣІзәҝEдәӨдәҺPгҖҒQдёӨзӮ№пјҢи®ҫN(0пјҢ
дёҺжӣІзәҝEдәӨдәҺPгҖҒQдёӨзӮ№пјҢи®ҫN(0пјҢ![]() )(
)(![]() <0)пјҢ
<0)пјҢ![]() дёҺ
дёҺ![]() зҡ„еӨ№и§’дёә
зҡ„еӨ№и§’дёә![]() пјҢиӢҘ
пјҢиӢҘ![]() вүӨ
вүӨ![]() зӯүжҒ’жҲҗз«ӢпјҢжұӮ
зӯүжҒ’жҲҗз«ӢпјҢжұӮ![]() зҡ„еҸ–еҖјиҢғеӣҙ;
зҡ„еҸ–еҖјиҢғеӣҙ;
(в…ў)и®ҫд»ҘзӮ№NдёәеңҶеҝғпјҢд»Ҙ![]() еҚҠеҫ„зҡ„еңҶдёҺжӣІзәҝEеңЁз¬¬дёҖиұЎйҷҗзҡ„дәӨзӮ№дёәHпјҢиӢҘеңҶеңЁзӮ№HеӨ„зҡ„еҲҮзәҝдёҺжӣІзәҝEеңЁзӮ№HеӨ„зҡ„еҲҮзәҝдә’зӣёеһӮзӣҙпјҢжұӮ
еҚҠеҫ„зҡ„еңҶдёҺжӣІзәҝEеңЁз¬¬дёҖиұЎйҷҗзҡ„дәӨзӮ№дёәHпјҢиӢҘеңҶеңЁзӮ№HеӨ„зҡ„еҲҮзәҝдёҺжӣІзәҝEеңЁзӮ№HеӨ„зҡ„еҲҮзәҝдә’зӣёеһӮзӣҙпјҢжұӮ![]() зҡ„еҖјпјҺ
зҡ„еҖјпјҺ

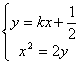 В В
В В 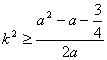
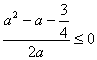 В
В