已知抛物线y2＝2px(p>0)的焦点F为双曲线
－
＝1(a>0，b>0)的一个焦点，经过两曲线交点的直线恰过点F，则该双曲线的离心率为( )
(A)
(B)1＋ (C)
(D)1＋
已知抛物线y2＝2px(p>0)的焦点F为双曲线－＝1(a>0，b>0)的一个焦点，经过两曲线交点的直线恰过点F，则该双曲线的离心率为( )
(A) (B)1＋ (C) (D)1＋
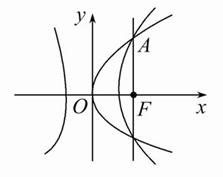B.∵抛物线与双曲线有共同的焦点，
∴
＝c，∴p＝2c.
又设A为两曲线的一个交点，
则A(，p)，即A(c,2c)，又A在双曲线上，
∴
－
＝1.
整理可得a4－6a2c2＋c4＝0，
∴e4－6e2＋1＝0，∴e2＝3＋2，∴e＝＋1.