如图所示，倾角为30°的光滑斜面上有一个质量为1Kg的物块，收到一个与斜面平行的大小为5N的外力F左
右，从A点由静止开始运动，下滑30cm后再B点与放置在斜面底部的轻弹簧接触并立刻撤去外力F，物块压缩弹簧最短至C点，然后原路返回，已知BC间的距离为20cm，g取10m/s2，下列说法中正确的是（ ）
|
| A． | 物块经弹簧反弹后恰好可以回到A点 |
|
| B． | 物块从A点到C点的运动过程中，克服弹簧的弹力做功为4J |
|
| C． | 物块从A点到C点的运动过程中，能达到的最大动能为3J |
|
| D． | 物块从A点到C点的运动过程中，物块与弹簧构成的系统机械能守恒 |
考点：
功能关系；验证机械能守恒定律．
分析：
通过分析小球的受力情况，来分析其运动情况，确定速度的变化，由功能关系分析，分析时要抓住弹簧的弹力与压缩量成正比．
解答：
解：A、下滑的过程中拉力F做功，系统的机械能增大，所以物块经弹簧反弹后恰好可以高于A点．故A错误；
B、物块从A点到C点的运动过程中，重力、拉力与弹簧的弹力做功，重力做功：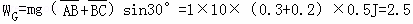
J
拉力做功：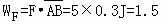
J，由于A点与C点的速度都是0，所以：W弹=﹣WG﹣WF=﹣2.5﹣1.5=﹣4J，即克服弹簧的弹力做功为4J．故B正确；
C、物体到达B时，拉力与重力做功：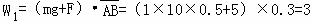
J，而经过B点后比较短的时间内由于重力沿斜面向下的分力大于弹簧的弹力所以物体要先做加速运动，一直到弹簧的弹力大于重力的分力，物体才做减速运动，所以物块从A点到C点的运动过程中，能达到的最大动能大于3J．故C错误；
D、物块从A点到C点的运动过程中，由于拉力做正功，物块与弹簧构成的系统机械能不守恒．故D错误．
故选：B
点评：
解决本题的关键是分析小球的受力情况，判断其运动情况，是常见的问题．