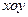 中,点
中,点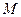 在
在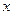 轴的正半轴上, ⊙
轴的正半轴上, ⊙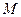 交
交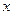 轴于
轴于 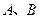 两点,交
两点,交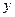 轴于
轴于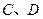 两点,且
两点,且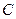 为
为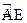 的中点,
的中点,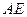 交
交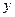 轴于
轴于 点,若点
点,若点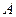 的坐标为(-2,0),
的坐标为(-2,0),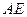
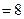

(1)(3分)求点
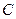 的坐标.
的坐标. (2)(3分)连结
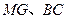 ,求证:
,求证: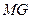 ∥
∥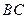
(3)(4分) 如图10-2,过点
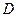 作⊙
作⊙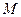 的切线,交
的切线,交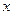 轴于点
轴于点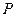 .动点
.动点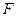 在⊙
在⊙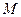 的圆周上运动时,
的圆周上运动时,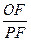 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律 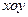 中,点
中,点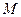 在
在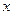 轴的正半轴上, ⊙
轴的正半轴上, ⊙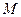 交
交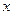 轴于
轴于 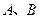 两点,交
两点,交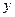 轴于
轴于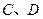 两点,且
两点,且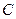 为
为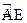 的中点,
的中点,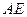 交
交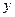 轴于
轴于 点,若点
点,若点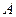 的坐标为(-2,0),
的坐标为(-2,0),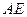
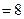

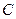 的坐标.
的坐标. 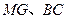 ,求证:
,求证: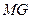 ∥
∥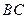
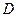 作⊙
作⊙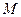 的切线,交
的切线,交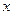 轴于点
轴于点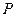 .动点
.动点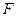 在⊙
在⊙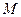 的圆周上运动时,
的圆周上运动时,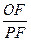 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律  解析:
解析: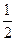 CD ……1分
CD ……1分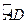 =
=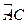
 的中点
的中点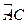 =
=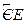
 =
=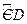
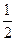 CD=4
CD=4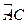 的中点,M为圆心
的中点,M为圆心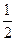 AE=4 ……1分
AE=4 ……1分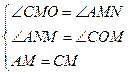
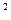 +OM
+OM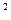 =MC
=MC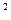 得:
得: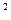 +(r-2)
+(r-2)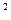 =r
=r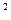
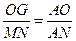
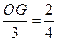
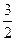 ……2分
……2分
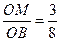

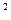 =MO·MP;
=MO·MP;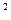 =OM·OP(说明:直接使用射影定理不扣分)
=OM·OP(说明:直接使用射影定理不扣分)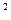 =3·OP
=3·OP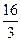 ……1分
……1分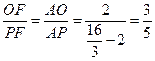
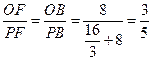 ……2分
……2分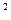 =MO·MP
=MO·MP =MO·MP
=MO·MP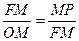
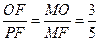
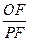 的比值不变,比值为
的比值不变,比值为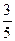 ……4分
……4分