已知四边形ABCD的外接圆⊙O的半径为5，对角线AC与BD的交点为E，且AB2=AE·AC，BD=8，
1.判断△ABD的形状并说明理由；
2.求△ABD的面积
已知四边形ABCD的外接圆⊙O的半径为5，对角线AC与BD的交点为E，且AB2=AE·AC，BD=8，
1.判断△ABD的形状并说明理由；
2.求△ABD的面积
1.△ABD是等腰三角形
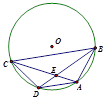
如图，连接OA、OB，交DB于F；
∵AB2=AE•AC，即
；
又∵∠BAE=∠CAB，
∴△ABE∽△ACB；
∴∠DBA=∠BCA；
而∠BCA=∠BDA，∴∠DBA=∠BDA；
∴AB=AD，
∴△ABD是等腰三角形。（4分）
2.∵AB=AD，
∴OA⊥BD，且F为BD的中点；
∴BF=4；
在Rt△BOF中，OB2=BF2+OF2，∴OF=3；
而OA=5，∴AF=2；
∴S△ABD=
BD×AF=8．（10分）
解析:求△ABD的面积，已知了底边BD的长，因此只需求出BD边上的高即可．连接OA、OB，交DB于F；已知AB2=AE•AC，易证得△ABE∽△ACB；可得∠BCA=∠DBA，即弧AD=弧AB，根据垂径定理，可知OA垂直平分BD；易求得OF=3，则AF=2，由此可求得△ABD的面积．