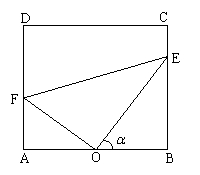
如图,有一块矩形草坪ABCD,AB=100米,BC=![]() 米,欲在这块草坪内铺设三条小路OE、EF和OF,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°;
米,欲在这块草坪内铺设三条小路OE、EF和OF,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°;
(1)设∠BOE=![]() ,试求
,试求![]() 的周长
的周长![]() 关于
关于![]() 的函数解析式,并求出此函数的定义域;
的函数解析式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为400元,试问如何设计才能使铺路的总费用最低?
并求出最低总费用.
如图,有一块矩形草坪ABCD,AB=100米,BC=![]() 米,欲在这块草坪内铺设三条小路OE、EF和OF,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°;
米,欲在这块草坪内铺设三条小路OE、EF和OF,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°;
(1)设∠BOE=![]() ,试求
,试求![]() 的周长
的周长![]() 关于
关于![]() 的函数解析式,并求出此函数的定义域;
的函数解析式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为400元,试问如何设计才能使铺路的总费用最低?
并求出最低总费用.

(1)Rt△BOE中,OB=50, ∠B=90°,∠BOE=![]() ,∴OE=
,∴OE=![]() .
.
Rt△AOF中,OA=50, ∠A=90°,∠AFO=![]() ,∴OF=
,∴OF=![]() .
.
又∠EOF=90°,∴EF=![]() =
=![]() ,
,
∴![]()
即![]() .
.
当点F在点D时,这时角![]() 最小,求得此时
最小,求得此时![]() =
=![]() ;
;
当点E在C点时,这时角![]() 最大,求得此时
最大,求得此时![]() =
=![]() .
.
故此函数的定义域为![]() .
.
(2)由题意知,要求铺路总费用最低,只要求![]() 的周长
的周长![]() 的最小值即可.
的最小值即可.
由(1)得,![]() ,
,![]()
设![]() ,则
,则![]() ,
,
∴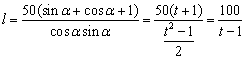 .
.
由,![]() ,得
,得![]() ,∴
,∴![]() ,
,
从而![]() ,当
,当![]() ,即BE=50时,
,即BE=50时,![]() ,
,
所以当BE=AE=50米时,铺路总费用最低,最低总费用为![]() 元.
元.