如图， Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E为BC边的中点，连接DE.
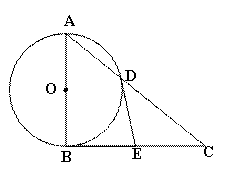（1）求证：DE与⊙O 相切.
（2）若tanC=
，DE=2，求AD的长．
如图， Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E为BC边的中点，连接DE.
（1）求证：DE与⊙O 相切.
（2）若tanC=，DE=2，求AD的长．
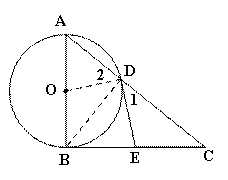
（1）证明：连接BD、OD，
∵AB为⊙O的直径，∴∠ADB=∠BDC=90°，
∵E为BC边的中点，∴DE=EC，∴∠1=∠C，∵OA=OD，∴∠2=∠A，
∵∠ABC=90°，∴∠A+∠C =90°，∴∠1+∠2 =90
°，
∴∠ODE =90°，∴OD⊥DE于点D，
∵以AB为直径的⊙O交AC于点D，∴D是半径的外端，
∴DE与⊙O 相切.
(2) ∵∠BDC=90°，E为BC边的中点，∴ 
，∵DE=2，∴BC=4，
在Rt△ABC中，tanC=
，
∴AB=BC·=2
，
在Rt△ABC中，
AC=
=
=6，
又∵△ABD∽△ACB，∴
，
即
，
∴AD=