，求x的值；（2）已知tanx=tan
，求x的值．
，求x的值；（2）已知tanx=tan，求x的值．
解法一：（1）在同一坐标系中作出y=cosx与y=cos的图象，如图.在（-π，π）上满足cosx=cos
的角有两个：
，-
.由y=cosx的周期为2π，则满足cosx=cos
的x为±
+2kπ，k∈Z
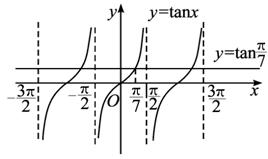
（2）在同一坐标系中作出y=tanx与y=tan
的图象，如图.在(-
，
)上满足tanx=tan
的x有且只有一个角
.又y=tanx的周期为π，则满足tanx=tan
的x=
+kπ，k∈Z
解法二：（1）在（-π，π）上满足cosx=cos
的角有两个：
，-
.由y=cosx的周期为2π，则满足cosx=cos
的x为±
+2kπ，k∈Z
（2）在(-
，
)上满足tanx=tan
的x有且只有一个角
.又y=tanx的周期为π，则满足tanx=tan
的x=
+kπ，k∈Z