在△ABC中,AC=6,BC=8,AB=10,点D、E分别在AB、AC上,且DE将△ABC的周长分成相等的两部分.设AE=x,AD=y,△ADE的面积为S.
(1)求出y关于x的函数关系式,并写出x的取值范围;
(2)求出S关于x的函数关系式;试判断S是否有最大值,若有,则求出其最大值,并指出此时△ADE的形状;若没有,请说明理由.
 |
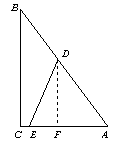
在△ABC中,AC=6,BC=8,AB=10,点D、E分别在AB、AC上,且DE将△ABC的周长分成相等的两部分.设AE=x,AD=y,△ADE的面积为S.
(1)求出y关于x的函数关系式,并写出x的取值范围;
(2)求出S关于x的函数关系式;试判断S是否有最大值,若有,则求出其最大值,并指出此时△ADE的形状;若没有,请说明理由.
 |
解:(1)∵DE平分△ABC的周长
∴![]() ,即y+x=12
,即y+x=12
∴y关于x的函数关系式为:y=12-x(2≤x≤6)
(2)过点D作DF⊥AC,垂足为F
∵![]() ,即
,即![]()
∴△ABC是直角三角形,∠ACB=90°
∴![]() ,即
,即![]()
∴![]()
∴![]()
![]()
故当x=6时,S取得最大值![]()
此时,y=12-6=6,即AE=AD.因此,△ADE是等腰三角形.
 |