如图(1)，四边形ABCD为矩形，PD⊥平面ABCD，AB=1，BC=PC=2，如图(2)所示折叠，折痕EF∥DC.其中点E，F分别在线段PD，PC上，沿EF折叠后点P在线段AD上的点记为M，并且MF⊥CF.
(1)求证：CF⊥平面MDF；
(2)求三棱锥M-CDE的体积.
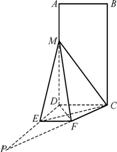
图(1) 图(2)
(例1)
如图(1)，四边形ABCD为矩形，PD⊥平面ABCD，AB=1，BC=PC=2，如图(2)所示折叠，折痕EF∥DC.其中点E，F分别在线段PD，PC上，沿EF折叠后点P在线段AD上的点记为M，并且MF⊥CF.
(1)求证：CF⊥平面MDF；
(2)求三棱锥M-CDE的体积.
图(1) 图(2)
(例1)
【解答】(1)因为PD⊥平面ABCD，PD
平面PCD，
所以平面PCD⊥平面ABCD，
而平面PCD∩平面ABCD=CD，
MD平面ABCD，MD⊥CD，
所以MD⊥平面PCD.
因为CF平面PCD，所以CF⊥MD，
又CF⊥MF，MD，MF平面MDF，且MD∩MF=M，
所以CF⊥平面MDF.
(2)由(1)知CF⊥平面MDF，
DF平面MDF，所以CF⊥DF，
易知∠PCD=60°，所以∠CDF=30°，
从而CF=
CD=，
因为EF∥DC，
所以
=
，即
=
，
所以DE=
，所以PE=
，
所以S△CDE=CD×DE=
，
MD=
=
=
=
，
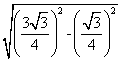所以
=
S△CDE×MD=××=
.
【精要点评】本题以折叠图形为考查形式，考查直线与平面垂直的判定以及利用等体积法计算三棱锥的体积，属于中档题.图形折叠问题主要先弄清量的变与不变的问题，以及两个图形之间的关系等.