已知，点M为二次函数y＝－(x－b)2＋4b＋1图象的顶点，直线y＝mx＋5分别交x的正半轴，y轴于点A，B.
(1)判断顶点M是否在直线y＝4x＋1上，并说明理由；
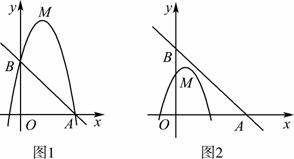
(2)如图1，若二次函数图象也经过点A，B，且mx＋5>－(x－b)2＋4b＋1.根据图象，写出x的取值范围；
(3)如图2，点A坐标为(5，0)，点M在△AOB内，若点C(
，y1)，D(
，y2)都在二次函数图象上，试比较y1与y2的大小．
已知，点M为二次函数y＝－(x－b)2＋4b＋1图象的顶点，直线y＝mx＋5分别交x的正半轴，y轴于点A，B.
(1)判断顶点M是否在直线y＝4x＋1上，并说明理由；
(2)如图1，若二次函数图象也经过点A，B，且mx＋5>－(x－b)2＋4b＋1.根据图象，写出x的取值范围；
(3)如图2，点A坐标为(5，0)，点M在△AOB内，若点C(，y1)，D(，y2)都在二次函数图象上，试比较y1与y2的大小．
解：(1)由题意知，点M的坐标是(b，4b＋1)，
∴把x＝b代入y＝4x＋1得y＝4b＋1，
∴点M在直线y＝4x＋1上．
(2)∵直线y＝mx＋5与y轴交于点B，
∴点B坐标为(0，5)．
又∵B(0，5)在抛物线上，
∴5＝－(0－b)2＋4b＋1，解得b＝2，
∴二次函数的表达式为y＝－(x－2)2＋9，
∴当y＝0时，得x1＝5，x2＝－1，∴A(5，0)．
观察图象可得，当mx＋5>－(x－b)2＋4b＋1时，
x的取值范围为x<0或x>5.
(3)如图，∵直线y＝4x＋1与直线AB交于点E，与y轴交于点F，
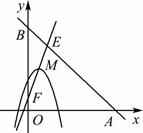
而直线AB的表达式为y＝－x＋5，
解方程组
∴点E(
，
)，F(0，1)．
点M在△AOB内，∴0<b<.
当点C，D关于抛物线对称轴对称时，
b－＝－b，∴b＝
，且二次函数图象的开口向下，顶点M在直线y＝4x＋1上．
综上所述，①当0<b<时，y1>y2；
②当b＝时，y1＝y2；
③当<b<时，y1<y2.