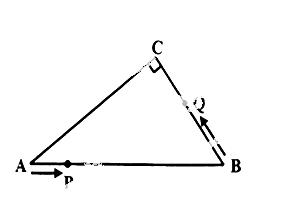
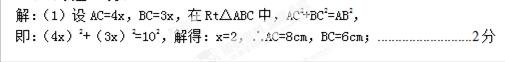如图，在Rt△ABC中，∠C=90°，AB=10cm，AC：BC=4：3，点P从点A出发沿AB方

如图，在Rt△ABC中，∠C=90°，AB=10cm，AC：BC=4：3，点P从点A出发沿AB方向向点B运动，速度为1cm/s，同时点Q从点B出发沿B→C→A方向向点A运动，速度为2cm/s，当一个运动点到达终点时，另一个运动点也随之停止运动．

（1）求AC、BC的长；

（2）设点P的运动时间为x（秒），△PBQ的面积为y（cm²），当△PBQ存在时，求y与x的函数关系式，并写出自变量x的取值范围；

（3）当点Q在CA上运动，使PQ⊥AB时，以点B、P、Q为定点的三角形与△ABC是否相似，请说明理由；

（4）当x=5秒时，在直线PQ上是否存在一点M，使得△BCM周长最小，若存在，求出最小周长，若不存在，请说明理由．

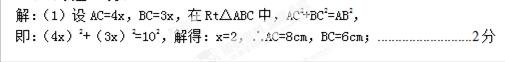
（2）①当点Q在边BC上运动时，过点Q作QH⊥AB于H，

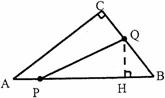
∵AP=x，∴BP=10﹣x，BQ=2x，∵△QHB∽△ACB，

∴，∴QH=错误！未找到引用源。x，y=错误！未找到引用源。BP•QH=（10﹣x） x=﹣x²+8x（0＜x≤3），......4分

②当点Q在边CA上运动时，过点Q作QH′⊥AB于H′，

∵AP=x，

∴BP=10﹣x，AQ=14﹣2x，∵△AQH′∽△ABC，

∴，即： ，解得：QH′= （14﹣2x），

∴y=PB•QH′=（10﹣x）•（14﹣2x）=x²﹣x+42（3＜x＜7）；

（3）∵AP=x，AQ=14﹣2x，

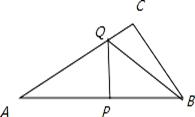
∵PQ⊥AB，∴△APQ∽△ACB，∴，即：  ，

解得：x=，PQ=，∴PB=10﹣x=，∴ 。PB:PQ=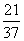BC:AC

∴当点Q在CA上运动，使PQ⊥AB时，以点B、P、Q为定点的三角形与△ABC不相似；

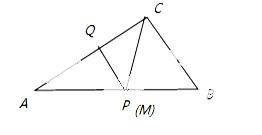
（4）存在．

理由：∵AQ=14﹣2x=14﹣10=4，AP=x=5，∵AC=8，AB=10，

∴PQ是△ABC的中位线，∴PQ∥CB，∴PQ⊥AC，

∴PQ是AC的垂直平分线，∴PC=AP=5，∴当点M与P重合时，△BCM的周长最小，

∴△BCM的周长为：MB+BC+MC=PB+BC+PC=5+6+5=16．∴△BCM的周长最小值为16．