（1）求△AOB面积的最小值及此时直线l的方程；
（2）求直线l在两坐标轴上的截距之和的最小值及此时直线的方程.
（1）求△AOB面积的最小值及此时直线l的方程；
（2）求直线l在两坐标轴上的截距之和的最小值及此时直线的方程.
（1）解法一：设A（a，0）、B（0，b）（显然a＞3）,则直线l的方程为
=1.把P（3，2）代入,得
+
=1,于是b=
,故△AOB的面积S=
ab=
=
=a-3+
+6=12.∴a-3=
,即a=6,b=4时,△AOB面积取最小值12.此时l的方程为
+
=1,即2x+3y-12=0.解法二：由1=
≥2
,得
≥2
，ab≥
.故△AOB的面积S=
ab≥12.当
=
=
,即a=6,b=4时,Smin=12.(以下同解法一)解法三：由b=
ab=
.去分母，得a2-Sa+3S=0.∵a为实数，∴Δ≥0，即S2-12S≥0.由S≥0得S≥12.将Smin=12代入上式，求得a=6，故b=4.(以下同解法一)
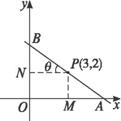
解法四：如上图所示，过P分别作x，y轴的垂线PM，PN（M、N为垂足），并设θ=∠PAM=∠BPN，则
S=S矩形PMON+S△PAM+S△PBN
=6+
×3×3×tanθ=6+2cotθ+
=12，∴当2cotθ=
时，Smin=12.(以下同解法一)（2）解法一：∵
=1，∴a+b=(
)（a+b）=3+
+
+2=
+
+5≥5+2
=5+2
.当
,即a=3+
,b=2+
时(a+b)min=5+2
,此时直线方程为(2+
)y-12-5
=0.解法二：∵a+b=(|OM|+|MA|)+(|ON|+|NB|)
=(3+2cotθ)+(2+3tanθ)=5+2cotθ+3tanθ≥5+2
=5+2
∴当2cotθ=3tanθ，即tanθ=
，b=2+
时，（a+b）min=5+2
，此时直线方程为（2+
）y-12-5
=0.深化升华
本题属“条件最值”问题，解题的总体思路是：先根据条件把多变元的函数减元化成单变元的目标函数，再根据表达式的结构特点确定最大、小值的求法.