(本小题满分13分)
已知椭圆![]() 的短轴长为
的短轴长为![]() ,且与抛物线
,且与抛物线![]() 有共同的焦点,椭圆
有共同的焦点,椭圆![]() 的左顶点为A,右顶点为
的左顶点为A,右顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() ,
,![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.
两点.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)求线段![]() 的长度的最小值;
的长度的最小值;
(Ⅲ)在线段![]() 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(本小题满分13分)
已知椭圆![]() 的短轴长为
的短轴长为![]() ,且与抛物线
,且与抛物线![]() 有共同的焦点,椭圆
有共同的焦点,椭圆![]() 的左顶点为A,右顶点为
的左顶点为A,右顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() ,
,![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.
两点.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)求线段![]() 的长度的最小值;
的长度的最小值;
(Ⅲ)在线段![]() 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(本小题满分13分)
解:(I)由已知得,抛物线的焦点为![]() ,则
,则![]() ,又
,又![]() .
.
由![]() ,可得
,可得![]() .
.
故椭圆![]() 的方程为
的方程为![]() .…………………………………………4分
.…………………………………………4分
(Ⅱ)直线![]() 的斜率
的斜率![]() 显然存在,且
显然存在,且![]() ,故可设直线
,故可设直线![]() 的方程为
的方程为![]() ,从而
,从而![]() .
.
由 得
得![]() .………………………………6分
.………………………………6分
设![]() ,则
,则![]() . 所以
. 所以![]() ,从而
,从而![]() .
.
即![]() 又
又![]() ,
,
则直线![]() 的斜率为
的斜率为![]() .
.
由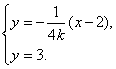 得
得![]()
所以![]() .
.
故![]() .
.
又![]() ,
, ![]() .
.
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
所以当![]() 时,线段
时,线段![]() 的长度取最小值
的长度取最小值![]() .…………………………………………8分
.…………………………………………8分
(Ⅲ)由(Ⅱ)可知,当![]() 的长度取最小值时,
的长度取最小值时,![]() .
.
则直线![]() 的方程为
的方程为![]() ,此时
,此时![]() ,
,![]() .
.
若椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 的面积等于
的面积等于![]() ,则点
,则点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,
,
所以![]() 在平行于
在平行于![]() 且与
且与![]() 距离等于
距离等于![]() 的直线
的直线![]() 上.
上.
设直线![]() .
.
则由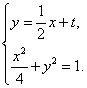 得
得![]() .………………………………………10分
.………………………………………10分
![]() .即
.即![]() .
.
由平行线间的距离公式,得 ![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
可求得![]() 或
或![]() .…………………………………………13分
.…………………………………………13分