(1)当a=0时，求A∩B；
(2)当a=1时，问是否存在自然数k和b，使得(A∩C)∪(B∩C)=
,若存在，求出k,b的值；若不存在，说明理由.
(1)当a=0时，求A∩B；
(2)当a=1时，问是否存在自然数k和b，使得(A∩C)∪(B∩C)=,若存在，求出k,b的值；若不存在，说明理由.
解析：(1)a=0,则A={(x,y)|x=-1,y∈R}.
由方程组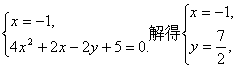
)};(2)a=1,则A中方程为y2-x-1=0,
∵A、B、C都是非空集合，由已知必有A∩C=
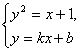,此即方程组
和方程组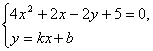
均无解.消去y整理得k2x2+(2bk-1)x+b2-1=0(k≠0)和4x2+2(1-k)x-2b+5=0,所以Δ1=（2bk-1）2-4k2(b2-1)=4k2-4kb+1＜0,且Δ2=4(1-k)2-16（5-2b）=4×（k2-2k+8b-19）＜0,从而Δ3=16b2-16＞0,且Δ4=4-4(8b-19)＞0,
∴b2＞1,且b＜
∴b=2,此时4k2-8k+1＜0,且k2-2k-3＜0,由此得
,k∈Z得k=1,即所求b=2,k=1.