在平面直角坐标系![]() 中,已知椭圆C的中心在原点O,焦点在
中,已知椭圆C的中心在原点O,焦点在![]() 轴上,短轴长为2,离心率为
轴上,短轴长为2,离心率为![]() .
.
(1)求椭圆C的方程;
(2)A、B为椭圆C上满足△AOB的面积为![]() 的任意两点, E为线段AB的中点,射线OE交椭圆C于点P,设
的任意两点, E为线段AB的中点,射线OE交椭圆C于点P,设![]() ,求实数t的值.
,求实数t的值.
在平面直角坐标系![]() 中,已知椭圆C的中心在原点O,焦点在
中,已知椭圆C的中心在原点O,焦点在![]() 轴上,短轴长为2,离心率为
轴上,短轴长为2,离心率为![]() .
.
(1)求椭圆C的方程;
(2)A、B为椭圆C上满足△AOB的面积为![]() 的任意两点, E为线段AB的中点,射线OE交椭圆C于点P,设
的任意两点, E为线段AB的中点,射线OE交椭圆C于点P,设![]() ,求实数t的值.
,求实数t的值.
解:(1)设椭圆C的方程为![]() ,由题意知
,由题意知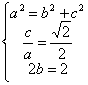 ,解得
,解得![]() ,椭圆C的方程为
,椭圆C的方程为![]() .
.
(2) 当AB⊥x轴时,设A(x0,y0),B(x0,-y0), 由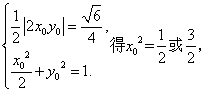
由![]() =t
=t![]() =t(x0,0)=(tx0,0),得P(tx0,0),又P在椭圆上,所以
=t(x0,0)=(tx0,0),得P(tx0,0),又P在椭圆上,所以![]() +02=1,所以t2=
+02=1,所以t2=![]() =4或
=4或![]() ,所以t=2或
,所以t=2或![]() (舍去负值).
(舍去负值).
当AB不垂直于x轴时,设AB:y=kx+m,显然m≠0,代入椭圆方程得(1+2k2)x2+4kmx+2(m2-1)=0.…(*)
由三角形面积公式知, ![]() |xAyB-xByA|=
|xAyB-xByA|=![]() |xA(kxB+m)-xB(kxA+m)|=
|xA(kxB+m)-xB(kxA+m)|=![]() |m||xA-xB|=
|m||xA-xB|=![]() ,
,
所以, ![]()
![]() ,
,
即![]() ,整理得,
,整理得, ![]() …①
…①
又![]() ,
,
所以, ![]() ,
,
即![]() ,将其代入椭圆方程得
,将其代入椭圆方程得 ,
,
整理可得,![]() ②
②
联立①②,消去![]() ,约分掉
,约分掉![]() ,移项整理得,
,移项整理得,![]() ,
,
解之可得,![]() 或
或![]() ,均能使
,均能使![]() 式的
式的![]() ,所以
,所以![]() 或
或![]() (舍去负值).
(舍去负值).
综上,![]() 或
或![]() .
.