在Rt△ACB中，∠ABC=90°，BC=6cm，AC=10cm．
（1）求AB的长．
（2）若点P从点B出发，以2cm/s的速度在BC所在的直线l上运动，设运动时间为t，那么当t为何值时，△ACP为等腰三角形？
在Rt△ACB中，∠ABC=90°，BC=6cm，AC=10cm．
（1）求AB的长．
（2）若点P从点B出发，以2cm/s的速度在BC所在的直线l上运动，设运动时间为t，那么当t为何值时，△ACP为等腰三角形？
【考点】勾股定理；等腰三角形的判定．
【专题】动点型．
【分析】（1）直接利用勾股定理计算AB长即可；
（2）此题要分四种情况：当P向左移动时：分CA=PA，AP=PC，PC=AC三种情况，当P向右移动时，AC=CP分别计算出t的值即可．
【解答】解：（1）∵∠ABC=90°，BC=6cm，AC=10cm，
∴AB=
=
=8（cm）；
（2）如图所示：
当P向左移动时，PB=2t，
若AP=AC=10cm，
则：BP=
=6（cm），
2t=6，
t=3；
若PC=AC=10cm，则BP=4cm，
2t=4，
解得：t=2；
若AP=PC，则PC=6+2t，AP=6+2t，
（2t）2+82=（6+2t）2，
解得：t=
，
当P向右移动时，BP=2t，则CP=2t﹣6，
当AC=CP时，2t﹣6=10，
解得：t=8．
答：当t为3，2，8huo时，△ACP为等腰三角形．
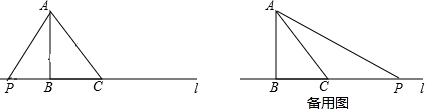
【点评】此题主要考查了勾股定理和等腰三角形的判定，关键是要分情况讨论，不要漏解．