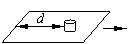
首页 / 一小圆盘静止在某一桌布上，桌布放在粗糙的水平地面上，圆盘距离

一小圆盘静止在某一桌布上，桌布放在粗糙的水平地面上，圆盘距离

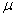
一小圆盘静止在某一桌布上，桌布放在粗糙的水平地面上，圆盘距离桌布左边边缘的距离为d，圆盘与桌布之间的动摩擦因数为，现用力向右水平拉动桌布。设桌布加速过程极短，可以认为桌布在抽动过程中一直做匀速直线运动。
试求：（1）小圆盘随桌布运动过程中加速度的可能值
（2）要将桌布从圆盘下抽出来，抽动桌布的速度v应满足什么条件？

答案

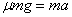
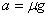
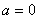
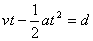
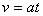
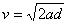
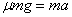
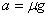
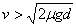
【解答】 (1)小圆盘在桌布上可能先加速后匀速，不滑离桌布；也可能只作加速运动就滑离桌布所以有： 加速过程 匀速过程 (2)圆盘滑到左端边缘，其速度就与桌布速度v相等，圆盘恰好不掉下．设桌布对地位移为s1，圆盘对地位移为s2． 有： 可得 由牛顿第二定律： 则只要桌布速度即可将桌布抽出来．

相关题目

-+-
-+-
针对漫画《极刑》，我们应该（   ）（漫画说明：人类生
针对漫画《极刑》，我们应该（   ）（漫画说明：人类生产生活大量排放二氧化碳，导致全球变暖，危及人类生存。）①要停止对自然资源的利用和
单项选择 从各题的四个选项中选出一个最佳答案。 Would you li
单项选择 从各题的四个选项中选出一个最佳答案。 Would you like some       ? Yes, a little please.      A. vegetables               B. carrot       
不等式组的整数解共有(  )A、2个         B．3个     
不等式组的整数解共有(  )A、2个         B．3个          C．4个          D．5个 
----- Would you mind if I put my book here?    -----_______!   A. Yes, go a
----- Would you mind if I put my book here?    -----_______!   A. Yes, go ahead     B. No, you’d better not   C. I’m sorry, but yes       D. I’m afraid not
新疆一个发展的禀赋，就是拥有众多自然资源。20世纪90年代
新疆一个发展的禀赋，就是拥有众多自然资源。20世纪90年代开始，新疆人就提出了“一黑一白一红”的三项发展战略。结合所学知识，回答下面试题。
在测电阻的实验中选用的器材及连接的部分电路如图所示。
在测电阻的实验中选用的器材及连接的部分电路如图所示。（1）请在方框内画出实验电路图，并把实物图连接完整。(2)实验中连接电路时，开关应_______
我国人大代表的素质不断提高，过去有的人大代表是当“哑
我国人大代表的素质不断提高，过去有的人大代表是当“哑巴代表”——有口不能说话；当“丫环代表”——当家不敢作主；当“举手代表”——与台

最新题目

蛔虫细胞和低等植物细胞共同具有的结构是           
—Have a good day! —________. A．No，it isn't              B．Good
通过宗法制的实行，西周形成一个庞大的宗族网。“大宗能
已知：①A是石油裂解气的主要成份，A的产量通常用来衡量一
为了了解学生关注热点新闻的情况，“两会”期间，小明对
 植物根毛细胞适于吸收水分的结构特点是(    )A.细胞壁极
已知数列{an}的前n项和Sn=n2（n∈N*）． （1）求数列{}的前10项
(2010·哈师大附中高三月考)某市政府广开言路，首创了“信访
中国人民银行是我国的中央银行，是全国金融业的管理机关
下列去括号错误的有（   ） ①m3－（2m－n－p）＝m3－2m＋n＋
阅读下列材料： 1923年12月17日北京大学25周年纪念日民意测验
由于铁丝在氧气中高温燃烧，部分熔化的铁没有及时反应便
秦朝建立的专制主义中央集权制度的本质特征是（    ）  
1．下列各组词语中，加点字的注音全都正确的一组是 A．聒
In England, afternoon tea, taken between four or five,          76____
下列关于不同等级城市服务范围的叙述，正确的是( ) A．上
Hardly ___ the door when the wind blew it open.     A. did I shut   B.I shu
目前，我国已经开始实施、具有战略性意义的、直接有利于
动物和人体内具有分裂和分化能力的细胞称为干细胞。对右
工业上制备H2的一种重要方法是： CO(g) + H2O(g)  CO2 (g) + H2(g)