如图所示，在U形容器内，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细绳的下端吊一个质量为m的小球(可视为质点)，球离底面的离度h＝L，当绳受到大小为3 mg的拉力时就会断裂．现让环与球一起以v＝
的速度向右运动，在A处环被挡住而立即停止，A离容器右壁的水平距离也为L.不计空气阻力，已知重力加速度为g.试求：
(1)在环被挡住而立即停止时绳对小球的拉力大小；
(2)在以后的运动过程中，球第一次碰撞容器的位置离B点的距离是多少？
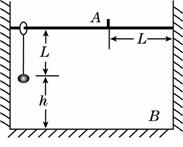
如图所示，在U形容器内，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细绳的下端吊一个质量为m的小球(可视为质点)，球离底面的离度h＝L，当绳受到大小为3 mg的拉力时就会断裂．现让环与球一起以v＝的速度向右运动，在A处环被挡住而立即停止，A离容器右壁的水平距离也为L.不计空气阻力，已知重力加速度为g.试求：
(1)在环被挡住而立即停止时绳对小球的拉力大小；
(2)在以后的运动过程中，球第一次碰撞容器的位置离B点的距离是多少？
解析 (1)在环被挡住而立即停止后小球立即以速度v绕A点做圆周运动，根据牛顿第二定律和圆周运动的向心力公式有：F－mg＝m
解得绳对小球的拉力大小为：F＝3 mg
(2)根据上面的计算可知，在环被A挡住的瞬间绳恰好断裂，此后小球做平抛运动．
假设小球直接落到底面上，则：h＝L＝
gt2
球的水平位移：x＝vt＝2L>L
所以小球先与右边的容器壁碰撞后再落到地面上
设球平抛运动到容器右壁的时间为t′，则t′＝
＝
，小球下落的高度h′＝gt′2＝
所以球第一次碰撞容器的位置距B的距离为：
s＝L－＝
L.
答案 (1)3 mg (2) L