小明喜欢研究问题，他将一把三角板的直角顶点放在平面直角坐标系的原点
处，两条直角边与抛物线
交于
、
两点．
1.（1）如左图，当
时，则
= ；
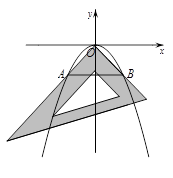
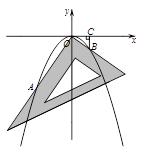
2.（2）对同一条抛物线，当小明将三角板绕点旋转到如右图所示的位置时，过点作
轴于点
，测得
，求出此时点的坐标；
3.（3）对于同一条抛物线，当小明将三角板绕点旋转任意角度时，他惊奇地发现，若三角板的两条直角边与抛物线有交点，则线段总经过一个定点，请直接写出该定点的坐标．
小明喜欢研究问题，他将一把三角板的直角顶点放在平面直角坐标系的原点处，两条直角边与抛物线交于、两点．
1.（1）如左图，当时，则= ；
2.（2）对同一条抛物线，当小明将三角板绕点旋转到如右图所示的位置时，过点作轴于点，测得，求出此时点的坐标；
3.（3）对于同一条抛物线，当小明将三角板绕点旋转任意角度时，他惊奇地发现，若三角板的两条直角边与抛物线有交点，则线段总经过一个定点，请直接写出该定点的坐标．
1.（1）．-
2.（2）由（1）可知抛物线的解析式为.
∵OC=1, ∴yB=, ∴B（1，
）．------2分
过点A作AD⊥x轴于点D， 又BC⊥x轴于点C，
∴∠ADO=∠BCO =90°． ∴∠1+∠2=90°．
∵AO⊥OB，∴∠1+∠3 =90°．∴∠2=∠3．
∴△DAO∽△COB．∴． ------3分
设点A坐标为（），则OD=-x，AD=
．
∴ , 解得x=-2, ∴yA=
,
故点A的坐标为(-2, )
3.（3）定点坐标是（0，）
解析:略