（本题满分13分）
投掷四枚不同的金属硬币
，假定
两枚正面向上的概率均为
，另两枚
为非均匀硬币，正面向上的概率均为
，把这四枚硬币各投掷一次，设
表示正面向上的枚数.
(Ⅰ)若出现一枚正面向上一枚反面向上与出现两枚正面均向上的概率相等，求
的值；
(Ⅱ)求的分布列及数学期望（用表示）；
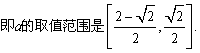
(Ⅲ)若出现2枚硬币正面向上的概率都不小于出现1枚和3枚硬币正面向上的概率，求的取值范围.
（本题满分13分）
投掷四枚不同的金属硬币，假定两枚正面向上的概率均为，另两枚为非均匀硬币，正面向上的概率均为，把这四枚硬币各投掷一次，设表示正面向上的枚数.
(Ⅰ)若出现一枚正面向上一枚反面向上与出现两枚正面均向上的概率相等，求的值；
(Ⅱ)求的分布列及数学期望（用表示）；
(Ⅲ)若出现2枚硬币正面向上的概率都不小于出现1枚和3枚硬币正面向上的概率，求的取值范围.
解：（Ⅰ）由题意，得
……………………3分
（Ⅱ）
=0，1，2，3，4. …………………4分
…………5分
；……………6分
……7分
…………………………8分
………………………………………9分
得的分布列为：
|
| 0 | 1 | 2 | 3 | 4 |
| p |
|
|
|
|
|
的数学期望为：
……10分
（Ⅲ）
≥0 .
≥0 .………12分
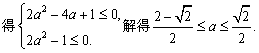
…13分
