我市在各校推广大阅读活动,初二(1)班为了解2月份全班学生课外
我市在各校推广大阅读活动,初二(1)班为了解2月份全班学生课外阅读的情况,调查了全班学生2月份读书的册数,并根据调查结果绘制了 如下不完整的条形统计图和扇形统计图:
如下不完整的条形统计图和扇形统计图:
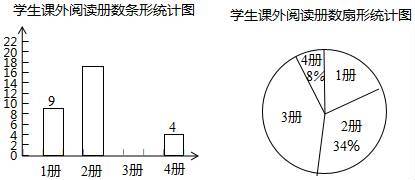
根据以上信息解决下列问题:
(1)参加本次问卷调查的学生共有 人,其中2月份读书2册的学生有 人;
(2)补全条形统计图,并求扇形统计图中读书3册所对应扇形的圆心角度数;
(3)在读书4册的学生中恰好有2名男生和2名女生,现要在这4名学生中随机选取2名学生参加学校的阅读分享沙龙,请用列举法(画树状图或列表)求所选取的这2名学生恰好性别相同的概率.
解:(1)∵本次调查的总人数为4÷8%=50人,
∴2月份读书2册的学生有50×34%=17(人),
故答案为:50、17;
(2)读书3册的人数为50﹣(9+17+4)=20,
补全统计图如下:
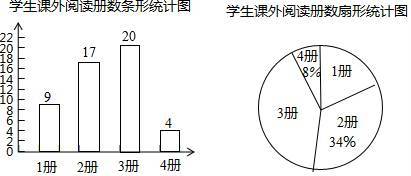
扇形统计图中读书3册所对应扇形的圆心角度数为360°×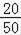 =144°;
=144°;
(3)列表得:
| | 男1 | 男2 | 女1 | 女2 |
| 男1 | ﹣﹣ | 男2男1 | 女1男1 | 女2男1 |
| 男2 | 男1男2 | ﹣﹣ | 女 1男2 1男2 | 女2男2 |
| 女1 | 男1女1 | 男2女1 | ﹣﹣ | 女2女1 |
| 女2 | 男1女2 | 男2女2 | 女1女2 | ﹣﹣ |
由表格可知,共有12种可能出现的结果,并且它们都是等可能的,其中这2名学生恰好性别相同的有4种可能.
所以这2名学生恰好性别相同的概率为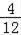 =
=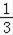 .
.
![]() 如下不完整的条形统计图和扇形统计图:
如下不完整的条形统计图和扇形统计图:

