①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题 .
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题 .
解析：
假设①③④为条件，即m⊥n,n⊥β,m⊥α成立，如下图,过m上一点P作PB∥n，则PB⊥m,PB⊥β，设垂足为B.
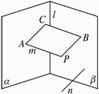又设m⊥α的垂足为A，
过PA、PB的平面与α、β的交线l交于点C，
因为l⊥PA,l⊥PB,所以l⊥平面PAB，得l⊥AC,l⊥BC,∠ACB是二面角α-l-β的平面角.
显然∠APB+∠ACB=180°，因为PA⊥PB，所以∠ACB=90°，得α⊥β.由①③④推得②成立.
反过来，如果②③④成立，与上面证法类似可得①成立.
答案：
m⊥α,n⊥β,α⊥β
m⊥n或m⊥n,m⊥α,n⊥β
α⊥β(二者任选一个即可).