已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE=DF，CE的延长线交DA的延长线于点G，CF的延长线交BA的延长线于点H．
（1）求证：△BEC∽△BCH；
（2）如果BE2=AB•AE，求证：AG=DF．
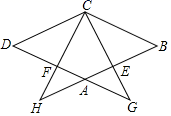
已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE=DF，CE的延长线交DA的延长线于点G，CF的延长线交BA的延长线于点H．
（1）求证：△BEC∽△BCH；
（2）如果BE2=AB•AE，求证：AG=DF．
（1）证明见解析；（2）证明见解析．
【分析】
(1)先证明△CDF≌△CBE，进而得到∠DCF=∠BCE，再由菱形对边CD
BH，得到∠H=∠DCF，进而∠BCE=∠H即可求解．
(2) 由BE2=AB•AE，得到
=
，再利用AGBC，平行线分线段成比例定理得到=
，再结合已知条件即可求解．
【详解】
解：(1)∵四边形ABCD是菱形，
∴CD=CB，∠D=∠B，CDAB．
∵DF=BE，
∴△CDF≌△CBE(SAS)，
∴∠DCF=∠BCE．
∵CDBH，
∴∠H=∠DCF，
∴∠BCE=∠H．且∠B=∠B，
∴△BEC∽△BCH．
(2)∵BE2=AB•AE，
∴=，
∵AGBC，
∴
=，
∴=，
∵DF=BE，BC=AB，
∴BE=AG=DF，
即AG=DF．
【点睛】
本题考查相似三角形的判定和性质，全等三角形的判定和性质，平行线分线段成比例定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．