 和半圆
和半圆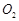 ,其中
,其中 和
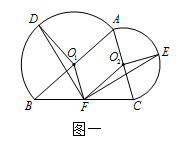
和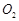 分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点. 【小题1】连结
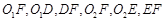 ,证明:
,证明: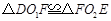 ;
;
【小题2】如图二,过点A分别作半圆
 和半圆
和半圆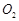 的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
【小题3】如图三,过点A作半圆
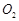 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆
的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆 的切线.
的切线.
 和半圆
和半圆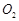 ,其中
,其中 和
和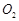 分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点. 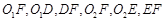 ,证明:
,证明: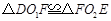 ;
;
 和半圆
和半圆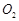 的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
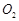 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆
的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆 的切线.
的切线.

 F=∠F
F=∠F E.
E. .
.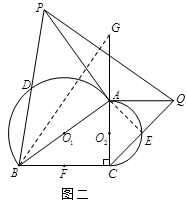
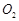 圆弧的中点,
圆弧的中点,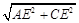 =
=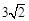 ,
,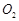 的切线,
的切线,
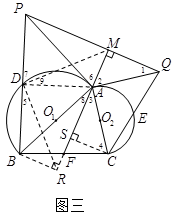
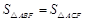 .
.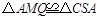 ,
,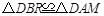 ,
,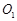 直径,
直径,

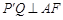 .
.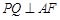 ,
,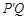 和
和 同时与AF垂直.
同时与AF垂直.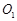 的切线.解析:
的切线.解析: