已知函数
．
（1）当
时，求函数
的单调区间；
（2）若函数
在
处取得极值，对
,
恒成立，求实数
的取值范围；
（3）当
时，求证：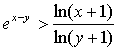
．
已知函数．
（1）当时，求函数的单调区间；
（2）若函数在处取得极值，对,恒成立，求实数的取值范围；
（3）当时，求证：．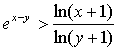
解：（1）
得0<x<
,
得x>
∴
在
上递减，在
上递增.
（2）∵函数在
处取得极值，∴
，
∴
，
令
，可得
在
上递减，在
上递增，
∴
，即
．
（3）证明：
，
令
，则只要证明
在
上单调递增，
又∵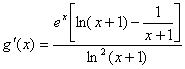
，
显然函数
在上单调递增．
∴
，即
，
∴在上单调递增，即
，
∴当
时，有
．