(本小题满分16分)
已知数列
满足
前
项和为
,
.
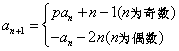（Ⅰ）若数列
满足
,试求数列前项和
；
（Ⅱ）若数列
满足
,试判断是否为等比数列,并说明理由；
（Ⅲ）当
时,问是否存在
,使得
,若存在,求出所有的的值；
若不存在，请说明理由.
(本小题满分16分)
已知数列满足前项和为,.
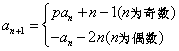（Ⅰ）若数列满足,试求数列前项和；
（Ⅱ）若数列满足,试判断是否为等比数列,并说明理由；
（Ⅲ）当时,问是否存在,使得,若存在,求出所有的的值；
若不存在，请说明理由.
解：（Ⅰ）据题意得
,所以
成等差数列,故
……………4分
（Ⅱ）当
时,数列
成等比数列；当
时,数列不为等比数列……………………5分
理由如下:因为
,
所以
,故当时,数列是首项为1,公比为
等比数列；
当时,数列不成等比数列 ………………………………………………………………… 9分
（Ⅲ）当时,
,
………………………………10分
因为
=
(
) ……………………………………………12分
，
，设
，
则
，
，且
，
在
递增，且
，
仅存在惟一的
使得
成立……………………………………………………16分