（2019·山东中考模拟）如图，双曲线y=
（x＞0）经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为（2，3），BE⊥x轴，垂足为E．
（1）确定k的值；
（2）若点D（3，m）在双曲线上，求直线AD的解析式；
（3）计算△OAB的面积．
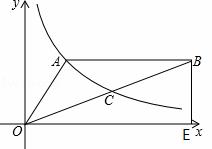
（2019·山东中考模拟）如图，双曲线y=（x＞0）经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为（2，3），BE⊥x轴，垂足为E．
（1）确定k的值；
（2）若点D（3，m）在双曲线上，求直线AD的解析式；
（3）计算△OAB的面积．
(1)k=6 (2) y=﹣x+5 (3) 9
【解析】
（1）将点A（2，3）代入解析式y=，
得：k=6；
（2）将D（3，m）代入反比例解析式y=
，
得：m=
=2，
∴点D坐标为（3，2），
设直线AD解析式为y=kx+b，
将A（2，3）与D（3，2）代入
得：
，
解得：
则直线AD解析式为y=-x+5；
（3）过点C作CN⊥y轴，垂足为N，延长BA，交y轴于点M，
∵AB∥x轴，
∴BM⊥y轴，
∴MB∥CN，
∴△OCN∽△OBM，
∵C为OB的中点，即
，
∴
，
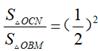∵A，C都在双曲线y=上，
∴S△OCN=S△AOM=3，
由
，
得：S△AOB=9，
则△AOB面积为9．