如图，在△ABC中，∠B=90°，AB=6㎝，BC=8㎝。点P从A开始沿AB边向点B以1㎝∕s的速度移动，点Q从点B开始沿BC边向点C以2㎝∕s的速度移动。若P、Q分别从A、B同时出发，
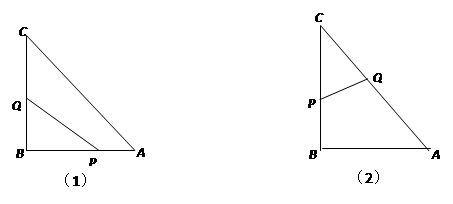
（1）如图（1），经过多少时间，△PBQ与△ABC相似？
（2）如图（2），当P到B后又继续在BC上前进，Q到C后又继续在CA上前进，经过多少时间，可以使得△CPQ的面积为12.6㎝2？
如图，在△ABC中，∠B=90°，AB=6㎝，BC=8㎝。点P从A开始沿AB边向点B以1㎝∕s的速度移动，点Q从点B开始沿BC边向点C以2㎝∕s的速度移动。若P、Q分别从A、B同时出发，
（1）如图（1），经过多少时间，△PBQ与△ABC相似？
（2）如图（2），当P到B后又继续在BC上前进，Q到C后又继续在CA上前进，经过多少时间，可以使得△CPQ的面积为12.6㎝2？
（1）经过
时，（2）经过7秒
解析:(1)设经过
秒,△PBQ与△ABC相似,则AP=,BP=
,BQ=
(1分)
①若△PBQ∽△ABC 
即
∴
(S)
②若△PBQ∽△CBA 
即
∴
(S)
∴经过时,△PBQ与△ABC相似.
(2)过Q作QD⊥BC于D点.
在△CDQ与△CBA中
∴△CDQ∽△CBA ∴
设经过
秒∴
∴
∴
在△CPQ中,QD⊥CP
∴
当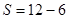
时 解得
.
当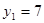
时,即经过7秒,P在BC上距点C7m处,Q在AC上距点C6m处.符合题意.
当
时,即经过11秒,P在BC上距点C3m处,而Q在AC上距点C14m处,不合题意,故舍去.
∴当经过7秒时,可以使△CPQ的面积为12.6cm2.