,过焦点F作直线交抛物线于A、B,且AF∶FB=1∶2.求(1)直线AB的方程;(2)弦AB中点到抛物线准线的距离. 
,过焦点F作直线交抛物线于A、B,且AF∶FB=1∶2.求(1)直线AB的方程;(2)弦AB中点到抛物线准线的距离. 思路分析：
由题目中的条件可知：利用直线的标准参数方程来求解,主要考虑从t的几何意义来入手解题.解：(1)由y=x2-2x+,得(x-1)2=y+
,∴焦点F（1,0）.可设直线AB:
代入y=x2-2x+
,∴t2cos2α-tsinα-
=0,由题意AF∶FB=1∶2,
∴
或
=-2,即t1=-
t2或t1=-2t2.
∴
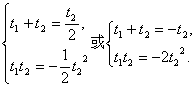
∴(t1+t2)2=-
t1t2或(t1+t2)2·(-2)=t1t2,解得tanα=±
.
∴AB:y=±
(x-1).
(2)设AB中点为M,AB: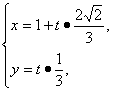
tm=
(t1+t2)=
·
,
∴
准线l:y=-
.∴d=ym-(-
)=
.