设数列{an}的前n项和Sn=na+n(n－1)b，(n=1,2,…),a、b是常数且b≠0.
(1)证明:{an}是等差数列.
(2)证明:以(an,
－1)为坐标的点Pn(n=1,2,…)都落在同一条直线上，并写出此直线的方程.
(3)设a=1,b=
,C是以(r,r)为圆心，r为半径的圆(r＞0)，求使得点P1、P2、P3都落在圆C外时，r的取值范围.
设数列{an}的前n项和Sn=na+n(n－1)b，(n=1,2,…),a、b是常数且b≠0.
(1)证明:{an}是等差数列.
(2)证明:以(an,－1)为坐标的点Pn(n=1,2,…)都落在同一条直线上，并写出此直线的方程.
(3)设a=1,b=,C是以(r,r)为圆心，r为半径的圆(r＞0)，求使得点P1、P2、P3都落在圆C外时，r的取值范围.
(1)证明略 (2)证明略(3)r的取值范围是(0，1)∪(1,
－
)∪(4+
,+∞)
由条件，得a1=S1=a,当n≥2时，
有an=Sn－Sn－1=［na+n(n－1)b］－［(n－1)a+(n－1)(n－2)b］=a+2(n－1)b.
因此，当n≥2时，有an－an－1=［a+2(n－1)b］－［a+2(n－2)b］=2b.
所以{an}是以a为首项，2b为公差的等差数列.
(2)证明:∵b≠0,对于n≥2,有
∴所有的点Pn(an,
－1)(n=1,2,…)都落在通过P1(a,a－1)且以
为斜率的直线上。 此直线方程为y－(a－1)= (x－a),即x－2y+a－2=0.
(3)解: 当a=1,b=时，Pn的坐标为(n,
),使P1(1,0)、P2(2, )、P3(3,1)都落在圆C外的条件是
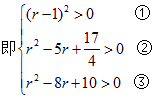
由不等式①,得r≠1
由不等式②，得r＜
－
或r＞+
由不等式③，得r＜4－
或r＞4+
再注意到r＞0,1＜－＜4－=+＜4+
故使P1、P2、P3都落在圆C外时，r的取值范围是(0，1)∪(1,－)∪(4+,+∞).