如图，已知二次函数y=ax2+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．
（1）求这个二次函数的表达式；
（2）若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．
①求线段PM的最大值；
②当△PCM是以PM为一腰的等腰三角形时，求点P的坐标．
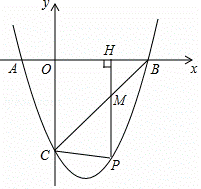
如图，已知二次函数y=ax2+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．
（1）求这个二次函数的表达式；
（2）若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．
①求线段PM的最大值；
②当△PCM是以PM为一腰的等腰三角形时，求点P的坐标．
【解答】解：（1）将A，B，C代入函数解析式，得
，
解得
，
这个二次函数的表达式y=x2﹣2x﹣3；
（2）设BC的解析是为y=kx+b，
将B，C的坐标代入函数解析式，得
，
解得
，
BC的解析是为y=x﹣3，
设M（n，n﹣3），P（n，n2﹣2n﹣3），
PM=（n﹣3）﹣（n2﹣2n﹣3）=﹣n2+3n=﹣（n﹣
）2+
，
当n=时，PM最大=；
②当PM=PC时，（﹣n2+3n）2=n2+（n2﹣2n﹣3+3）2，
解得n1=0（不符合题意，舍），n2=﹣
（不符合题意，舍），n3=，
n2﹣2n﹣3=2﹣2﹣3=﹣2﹣1，
P（，﹣2
﹣1）．
当PM=MC时，（﹣n2+3n）2=n2+（n﹣3+3）2，
解得n1=0（不符合题意，舍），n2=﹣7（不符合题意，舍），n3=1，
n2﹣2n﹣3=1﹣2﹣3=﹣4，
P（1，﹣4）；
综上所述：P（1，﹣4）或（，﹣2﹣1）．