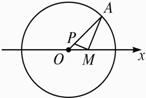

解:以O为极点,射线OM为极轴,建立极坐标系,如图.
设定圆O的半径为r,OM=a,P(ρ,θ)是轨迹上任意一点.
∵MP⊥MA,∴|MA|2+|MP|2=|PA|2,由余弦定理可知|MA|2=a2+r2-2arcosθ,|MP|2=a2+ρ2-2aρcosθ,而|PA|=r-ρ,由此可得
a2+r2-2arcosθ+a2+ρ2-2aρcosθ=(r-ρ)2,整理化简,得ρ=![]()
点评:寻找一个关键三角形,使动点的极半径和极角与已知条件成为该三角形的元素,借助于三角形的边角关系建立起动点的轨迹方程,这种方法称为三角形法.若三角形为直角三角形,可利用勾股定理及其他边角关系建立动点的极坐标方程;若三角形为一般三角形,可利用正、余弦定理建立动点的极坐标方程.