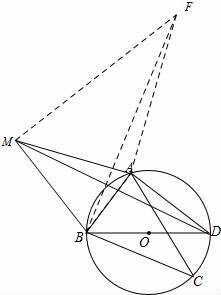
еҰӮеӣҫпјҢзӮ№Cдёәв–іABDзҡ„еӨ–жҺҘеңҶдёҠзҡ„дёҖеҠЁзӮ№пјҲзӮ№CдёҚеңЁ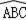
 дёҠпјҢдё”дёҚдёҺзӮ№BпјҢDйҮҚеҗҲпјүпјҢвҲ ACB=вҲ ABD=45°                  В
дёҠпјҢдё”дёҚдёҺзӮ№BпјҢDйҮҚеҗҲпјүпјҢвҲ ACB=вҲ ABD=45°                  В
пјҲ1пјүжұӮиҜҒпјҡBDжҳҜиҜҘеӨ–жҺҘеңҶзҡ„зӣҙеҫ„пјӣВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҲ2пјүиҝһз»“CDпјҢжұӮиҜҒпјҡ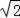
 В AC=BC+CDпјӣВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В AC=BC+CDпјӣВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҲ3пјүиӢҘв–іABCе…ідәҺзӣҙзәҝABзҡ„еҜ№з§°еӣҫеҪўдёәв–іABMпјҢиҝһжҺҘDMпјҢиҜ•жҺўз©¶DM2пјҢAM2пјҢBM2дёүиҖ…д№Ӣй—ҙж»Ўи¶ізҡ„зӯүйҮҸе…ізі»пјҢ并иҜҒжҳҺдҪ зҡ„з»“и®әпјҺВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В

 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
и§ЈпјҡпјҲ1пјүвҲө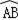
 =
=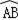
 пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ ACB=вҲ ADB=45В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲөвҲ ABD=45В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ BAD=90В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙBDжҳҜв–іABDеӨ–жҺҘеңҶзҡ„зӣҙеҫ„пјӣВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҲ2пјүеңЁCDзҡ„延й•ҝзәҝдёҠжҲӘеҸ–DE=BCпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
иҝһжҺҘEAпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲөвҲ ABD=вҲ ADBпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙAB=ADпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲөвҲ ADE+вҲ ADC=180В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲ ABC+вҲ ADC=180В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ ABC=вҲ ADEпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
еңЁв–іABCдёҺв–іADEдёӯпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В

 пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙв–іABCвүҢв–іADEпјҲSASпјүпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ BAC=вҲ DAEпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ BAC+вҲ CAD=вҲ DAE+вҲ CADпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ BAD=вҲ CAE=90В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲө
 =
=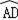
 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ ACD=вҲ ABD=45В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙв–іCAEжҳҜзӯүи…°зӣҙи§’дёүи§’еҪўпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙ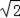
 AC=CEпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
AC=CEпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙ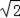
 AC=CD+DE=CD+BCпјӣВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
AC=CD+DE=CD+BCпјӣВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҲ3пјүиҝҮзӮ№MдҪңMFвҠҘMBдәҺзӮ№MпјҢиҝҮзӮ№AдҪңAFвҠҘMAдәҺзӮ№AпјҢMFдёҺAFдәӨдәҺзӮ№FпјҢиҝһжҺҘBFпјҢВ В В В В В В В В В В В В В В В В В
з”ұеҜ№з§°жҖ§еҸҜзҹҘпјҡвҲ AMB=ACB=45В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ FMA=45В°пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙв–іAMFжҳҜзӯүи…°зӣҙи§’дёүи§’еҪўпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙAM=AFпјҢMF=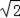
 AMпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
AMпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲөвҲ MAF+вҲ MAB=вҲ BAD+вҲ MABпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙвҲ FAB=вҲ MADпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
еңЁв–іABFдёҺв–іADMдёӯпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
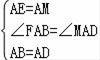
 пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙв–іABFвүҢв–іADMпјҲSASпјүпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙBF=DMпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
еңЁRtв–іBMFдёӯпјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲөBM2+MF2=BF2пјҢВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
вҲҙBM2+2AM2=DM2пјҺВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В

 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
гҖҗзӮ№иҜ„гҖ‘жң¬йўҳиҖғжҹҘеңҶзҡ„з»јеҗҲй—®йўҳпјҢж¶үеҸҠеңҶе‘Ёи§’е®ҡзҗҶпјҢзӯүи…°дёүи§’еҪўзҡ„жҖ§иҙЁпјҢе…Ёзӯүдёүи§’еҪўзҡ„жҖ§иҙЁдёҺеҲӨе®ҡпјҢеӢҫиӮЎе®ҡзҗҶзӯүзҹҘиҜҶпјҢз»јеҗҲзЁӢеәҰиҫғй«ҳпјҢи§ЈеҶіжң¬йўҳзҡ„е…ій”®е°ұжҳҜжһ„йҖ зӯүи…°зӣҙи§’дёүи§’еҪўпјҺВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
гҖҖВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
![]()
![]() дёҠпјҢдё”дёҚдёҺзӮ№BпјҢDйҮҚеҗҲпјүпјҢвҲ ACB=вҲ ABD=45°                  В
дёҠпјҢдё”дёҚдёҺзӮ№BпјҢDйҮҚеҗҲпјүпјҢвҲ ACB=вҲ ABD=45°                   ![]()
![]() В AC=BC+CDпјӣВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В AC=BC+CDпјӣВ В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В 
 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В 



 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В 
 В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В