еҰӮеӣҫпјҢеңЁе№ійқўзӣҙи§’еқҗж Үзі»xOyдёӯпјҢд»ҘMдёәйЎ¶зӮ№зҡ„жҠӣзү©зәҝдёҺxиҪҙеҲҶеҲ«зӣёдәӨдәҺBпјҢCдёӨзӮ№пјҢжҠӣзү©зәҝдёҠдёҖзӮ№Aзҡ„жЁӘеқҗж Үдёә2пјҢиҝһжҺҘABпјҢACпјҢжӯЈж–№еҪўDEFGзҡ„дёҖиҫ№GFеңЁзәҝж®өBCдёҠпјҢзӮ№DпјҢEеңЁзәҝж®өABпјҢACдёҠпјҢAKвҠҘxиҪҙдәҺзӮ№KпјҢдәӨDEдәҺзӮ№HпјҢдёӢиЎЁз»ҷеҮәдәҶиҝҷжқЎжҠӣзү©зәҝдёҠйғЁеҲҶзӮ№пјҲxпјҢyпјүзҡ„еқҗж ҮеҖјпјҡ
| x | вҖҰ | п№Ј2 | 0 | 4 | 8 | 10 | вҖҰ |
| y | вҖҰ | 0 | 5 | 9 | 5 | 0 | вҖҰ |
пјҲ1пјүжұӮеҮәиҝҷжқЎжҠӣзү©зәҝзҡ„и§ЈжһҗејҸпјӣ
пјҲ2пјүжұӮжӯЈж–№еҪўDEFGзҡ„иҫ№й•ҝпјӣ
пјҲ3пјүиҜ·й—®еңЁжҠӣзү©зәҝзҡ„еҜ№з§°иҪҙдёҠжҳҜеҗҰеӯҳеңЁзӮ№PпјҢеңЁxиҪҙдёҠжҳҜеҗҰеӯҳеңЁзӮ№QпјҢдҪҝеҫ—еӣӣиҫ№еҪўADQPзҡ„е‘Ёй•ҝжңҖе°ҸпјҹиӢҘеӯҳеңЁпјҢиҜ·жұӮеҮәPпјҢQдёӨзӮ№зҡ„еқҗж ҮпјӣиӢҘдёҚеӯҳеңЁпјҢиҜ·иҜҙжҳҺзҗҶз”ұпјҺ

В
и§ЈпјҡпјҲ1пјүз”ұеӣҫиЎЁеҸҜеҫ—пјҡжҠӣзү©зәҝзҡ„йЎ¶зӮ№еқҗж ҮдёәпјҡпјҲ4пјҢ9пјүпјҢ
и®ҫеҮҪж•°и§ЈжһҗејҸдёәпјҡy=aпјҲxп№Ј4пјү2 +9пјҲaвү 0пјүпјҢ
+9пјҲaвү 0пјүпјҢ
жҠҠзӮ№пјҲ0пјҢ5пјүд»Је…Ҙy=aпјҲxп№Ј4пјү2+9пјҢ
и§Јеҫ—пјҡa=п№Ј пјҺ
пјҺ
вҲҙеҮҪж•°и§ЈжһҗејҸдёәпјҡy=п№Ј пјҲxп№Ј4пјү2+9пјӣ
пјҲxп№Ј4пјү2+9пјӣ
пјҲ2пјүи®ҫжӯЈж–№еҪўDEFGзҡ„иҫ№й•ҝдёәmпјҢ
вҲөAKвҠҘxиҪҙпјҢ
вҲҙвҲ AKC=90В°пјҢ
вҲөвҲ DEF=вҲ EFG=90В°пјҢ
вҲҙеӣӣиҫ№еҪўHEFKдёәзҹ©еҪўпјҢ
вҲҙHK=EF=mпјҢ
вҲөзӮ№AеңЁжҠӣзү©зәҝy=п№Ј пјҲxп№Ј4пјү2+9дёҠпјҢжЁӘеқҗж Үдёә2пјҢ
пјҲxп№Ј4пјү2+9дёҠпјҢжЁӘеқҗж Үдёә2пјҢ
вҲҙy=п№Ј пјҲxп№Ј4пјү2+9=8пјҢ
пјҲxп№Ј4пјү2+9=8пјҢ
вҲҙзӮ№Aзҡ„еқҗж ҮдёәпјҡпјҲ2пјҢ8пјүпјҢ
вҲҙAK=8пјҢвҲҙAH=AKп№ЈHK=8п№ЈmпјҢ
з”ұйўҳж„ҸеҸҜеҫ—пјҡBпјҲп№Ј2пјҢ0пјүпјҢCпјҲ10пјҢ0пјүпјҢ
вҲҙBC=12пјҢ
вҲөDEвҲҘBCпјҢ
вҲҙв–іADEвҲҪв–іABCпјҢ
вҲҙ =
= пјҢ
пјҢ
вҲҙ =
= пјҢ
пјҢ
вҲҙm=п№Ј пјҢ
пјҢ
вҲҙжӯЈж–№еҪўзҡ„иҫ№й•ҝдёәпјҡ пјӣ
пјӣ
пјҲ3пјүеӯҳеңЁпјҢ
зҗҶз”ұпјҡиҝҮйЎ¶зӮ№MдҪңжҠӣзү©зәҝзҡ„еҜ№з§°иҪҙзӣҙзәҝlпјҡx=4пјҢ
и®ҫзӮ№Aе…ідәҺзӣҙзәҝlпјҡx=4еҜ№з§°зӮ№дёәAвҖІпјҢAвҖІзӮ№зҡ„еқҗж ҮдёәпјҡпјҲ6пјҢ8пјүпјҢ
вҲҙи®ҫABжүҖеңЁзӣҙзәҝи§ЈжһҗејҸдёәпјҡy=kx+bпјҢ
вҲҙ пјҢ
пјҢ
и§Јеҫ—пјҡ пјҢ
пјҢ
вҲҙABжүҖеңЁзӣҙзәҝи§ЈжһҗејҸдёәпјҡy=2x+4пјҢ
вҲөDеңЁзӣҙзәҝABдёҠпјҢDG= пјҢ
пјҢ
вҲҙзӮ№Dзҡ„зәөеқҗж Үдёәпјҡ пјҢ
пјҢ
з”ұ2x+4= пјҢ
пјҢ
и§Јеҫ—пјҡx= пјҢ
пјҢ
вҲҙзӮ№Dзҡ„еқҗж ҮдёәпјҡпјҲ пјҢ
пјҢ пјүпјҢ
пјүпјҢ
и®ҫзӮ№Dе…ідәҺxиҪҙеҜ№з§°зӮ№дёәDвҖІпјҢеҲҷDвҖІпјҲ пјҢп№Ј
пјҢп№Ј пјүпјҢ
пјүпјҢ
иҝһжҺҘAвҖІDвҖІдәӨеҜ№з§°иҪҙдәҺзӮ№PпјҢдәӨxиҪҙдәҺзӮ№QпјҢиҝһжҺҘAPпјҢDQпјҢ
еҲҷеӣӣиҫ№еҪўADQPзҡ„е‘Ёй•ҝжңҖе°ҸпјҢ
и®ҫзӣҙзәҝAвҖІDвҖІзҡ„и§ЈжһҗејҸдёәпјҡy=kвҖІx+bвҖІпјҢ
вҲҙ пјҢ
пјҢ
и§Јеҫ—пјҡ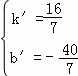 пјҢ
пјҢ
вҲҙзӣҙзәҝAвҖІDвҖІзҡ„и§ЈжһҗејҸдёәпјҡy= xп№Ј
xп№Ј пјҢ
пјҢ
еҪ“x=4ж—¶пјҢy= Г—4п№Ј
Г—4п№Ј =
= пјҢвҲҙPпјҲ4пјҢ
пјҢвҲҙPпјҲ4пјҢ пјүпјҢ
пјүпјҢ
еҪ“y=0ж—¶пјҢx= пјҢ
пјҢ
вҲҙQзӮ№еқҗж ҮдёәпјҡпјҲ пјҢ0пјүпјҺ
пјҢ0пјүпјҺ

В